통계 - 분포, 정규분포, 왜도, 첨도

04 Aug 2025 | Statistics

개인공부 후 자료를 남기기 위한 목적임으로 내용 상에 오류가 있을 수 있습니다.

분포

데이터가 전체 범위에서 어떻게 퍼져있는지를 나타내는 패턴

어떤 값 주변에 데이터가 얼마나 자주 등장하는지
데이터들이 어디에 몰려있는지 등을 설명함

왜 분포를 봐야 하는가?

평균이나 중앙값 등 단일 수치만으로는 데이터의 전체 모습을 알 수 없다
서로 다른 두 데이터가 같은 평균을 가질수는 있지만, 데이터의 퍼짐형태(=분포)는 전혀 다를수 있다

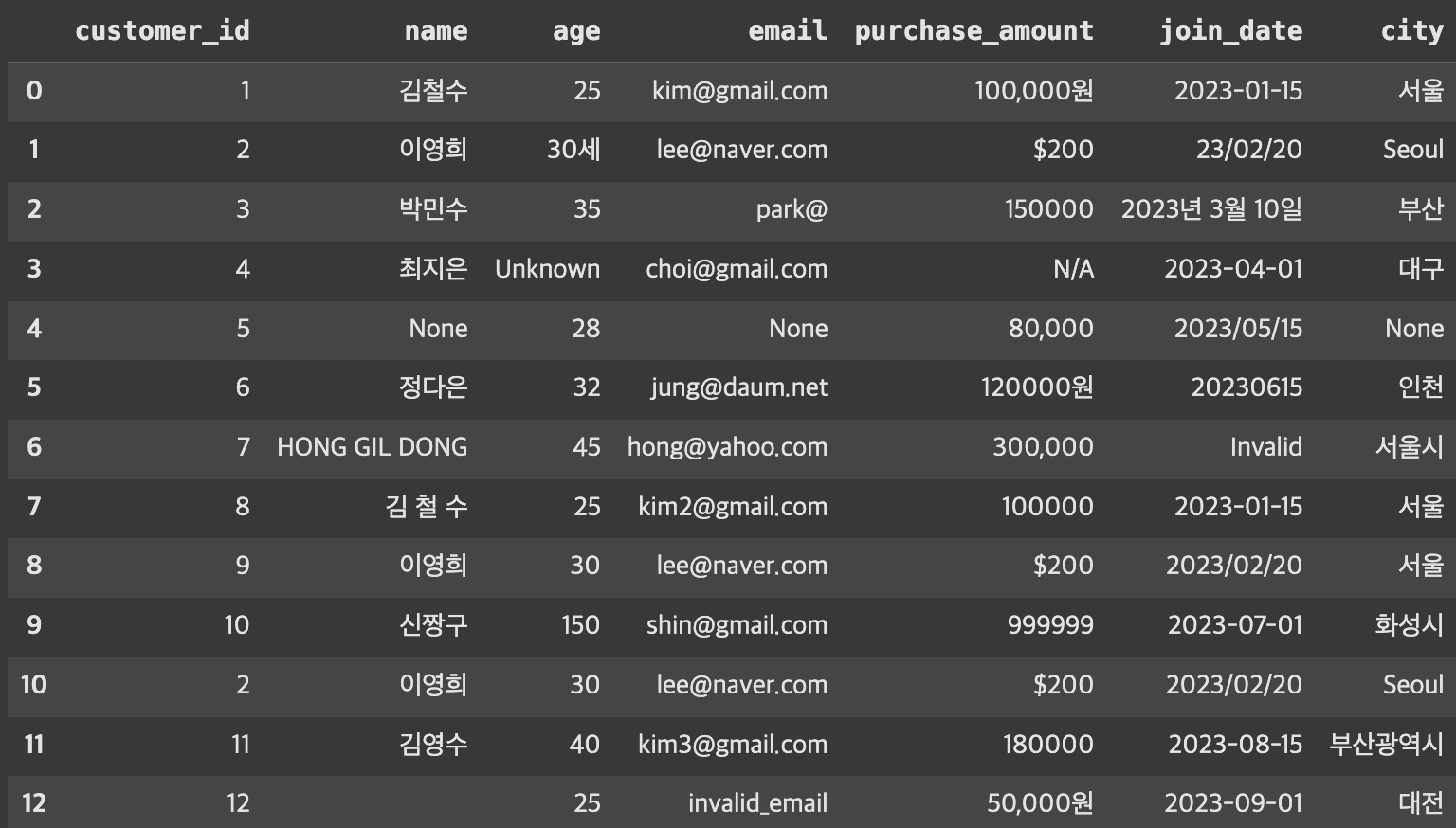
예시

A의 시험 점수
- $70, 71, 69, 70, 70, 71, 69, 70$
- 대부분 70 근처에 몰려 있음 → 집중된 분포
B의 시험 점수
- $40, 60, 80, 90, 70, 50, 100, 30$
- 점수가 넓게 퍼져 있음 → 흩어진 분포
둘 다 평균은 비슷하지만 분포는 매우 다름.

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

np.random.seed(0)

# A: 평균 70, 표준편차 1 (집중된 분포)
score_A = np.random.normal(loc=70, scale=3, size=1000)

# B: 평균 70, 표준편차 15 (넓게 퍼진 분포)
score_B = np.random.normal(loc=70, scale=8, size=1000)

plt.figure(figsize=(10, 5))

# 히스토그램 (확률 밀도 기준)
sns.histplot(score_A, kde=False, stat="density", bins=20, color="steelblue", label="A", alpha=0.3)
sns.histplot(score_B, kde=False, stat="density", bins=20, color="orange", label="B", alpha=0.3)

# KDE 선 그래프
sns.kdeplot(score_A, color="blue", linewidth=2)
sns.kdeplot(score_B, color="darkorange", linewidth=2)

plt.title("Score Distribution: A vs B (n=100)")
plt.xlabel("Score")
plt.ylabel("Density")
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()

정규분포(Normal Distribution)

데이터가 평균을 중심으로 좌우 대칭으로 퍼지는 분포
그래프 형태가 종(bell) 모양을 가짐 > bell curve라고도 불림
많은 자연현상과 측정값, 사람의 키, 시험 점수 등이 정규분포를 따름

정규분포의 특징

평균, 중앙값, 최빈값이 모두 같음
좌우가 대칭
대부분의 데이터가 평균 근처에 몰려있음
멀어질수록 빈도가 떨어짐
종 모양 곡선을 그릴 수 있음

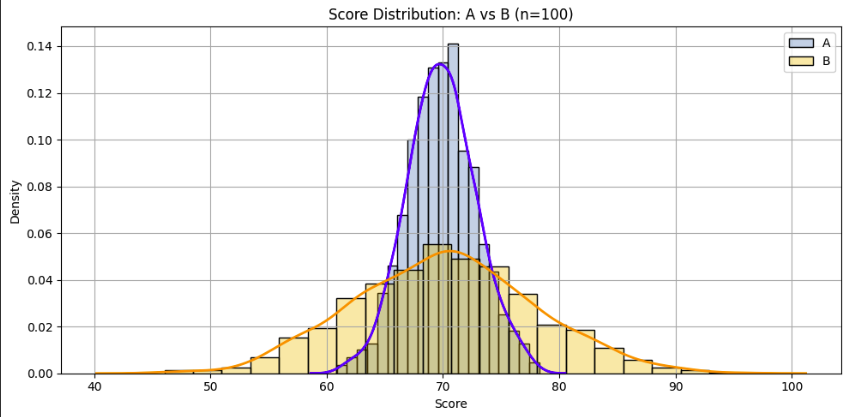
정규분포의 확률 분포 규칙 (68-95-99.7법칙)

평균 ± 1 표준편차 범위에 전체의 약 68% 포함
평균 ± 2 표준편차 → 약 95%
평균 ± 3 표준편차 → 약 99.7% → 이 범위 안에 대부분의 데이터가 있다는 의미

정규분포가 중요한 이유

많은 통계 분석 기법이 정규분포를 전제로 함(t-test, 회귀분석 등)
정규분포 위에서는 확률계싼, 이상값 판단, 신뢰구간 해석이 가능함
정규성을 만족하지 않으면 일반적인 검정 결과가 왜곡될 수 있음

정규분포는 평균이 곡선의 위치를 결정하고
표준편차가 곡선의 넓이와 뾰족함 정도를 결정

왜도(Skewness)

데이터 분포가 평균을 기준으로 좌우 대칭인지, 어느 한쪽으로 치우쳐있는 지를 나타내는 지표

정규분포의 왜도는 0, 완전한 대칭
하지만 데이터는 한쪽으로 더 몰리거나 꼬리가 길어지는 경우가 많음
왜도 > 분포가 얼마나 비대칭적으로 기울어져 있는지를 측정하는 정도

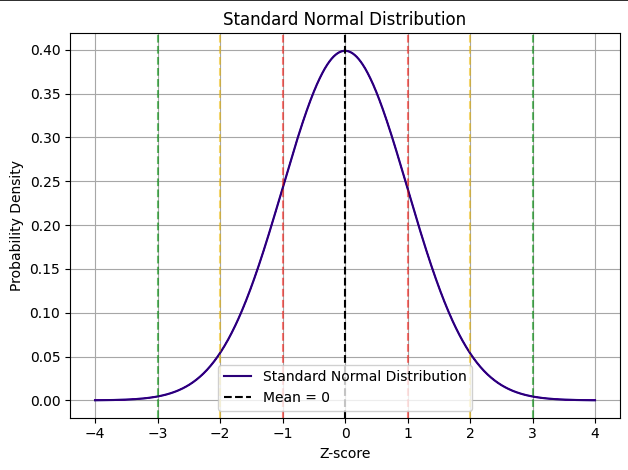
왜도의 종류

왜도 값	형태	설명
왜도 < 0	왼쪽 꼬리가 길다	음의 왜도, 평균 < 중앙값
왜도 = 0	좌우 대칭	정규분포에 가까움
왜도 > 0	오른쪽 꼬리가 길다	양의 왜도, 평균 > 중앙값

from scipy.stats import skew

np.random.seed(0)

# 데이터 생성
data_left = skewnorm.rvs(a=-6, size=1000) * 10 + 50   # 음의 왜도
data_normal = np.random.normal(loc=50, scale=10, size=1000)  # 정규
data_right = skewnorm.rvs(a=6, size=1000) * 10 + 50    # 양의 왜도

# 왜도 값 출력
print("Negative skew:", skew(data_left))
print("Symmetric:", skew(data_normal))
print("Positive skew:", skew(data_right))

# 시각화
fig, axes = plt.subplots(1, 3, figsize=(18, 5))

# 음의 왜도
sns.histplot(data_left, bins=30, kde=True, color='skyblue', ax=axes[0])
axes[0].set_title("Negative Skew")
axes[0].set_xlabel("Value")
axes[0].set_ylabel("Density")
axes[0].grid(True)

# 대칭
sns.histplot(data_normal, bins=30, kde=True, color='lightgreen', ax=axes[1])
axes[1].set_title("Symmetric")
axes[1].set_xlabel("Value")
axes[1].set_ylabel("Density")
axes[1].grid(True)

# 양의 왜도
sns.histplot(data_right, bins=30, kde=True, color='salmon', ax=axes[2])
axes[2].set_title("Positive Skew")
axes[2].set_xlabel("Value")
axes[2].set_ylabel("Density")
axes[2].grid(True)

plt.tight_layout()
plt.show()

첨도(Kurtosis)

분포의 뽀족함 또는 꼬리의 두꺼움 정도를 수치로 나타낸 값

정규 첨도: 정규분포처럼 적당히 뾰족하고 꼬리가 적당히 얇은 경우
고첨도: 중심에 데이터가 지나치게 몰려잇고 꼬리가 두꺼운 경우
저첨도: 분포가 평평하고 중앙 집중도가 낮은 경우

첨도의 종류

구분	첨도 값 (Fisher 기준)	형태	설명
고첨도	> 0	뾰족하고 꼬리가 두꺼움	이상치 발생 가능성이 높음
정규 첨도	= 0	정규분포와 동일한 형태	기준값 (표준 정규분포)
저첨도	< 0	평평하고 중심 집중도 낮음	꼬리가 얇고 극단값이 드묾

from scipy.stats import kurtosis

np.random.seed(1)

# 고첨도: t-distribution (자유도 3)
data_high = np.random.standard_t(df=3, size=1000)

# 정규첨도
data_normal = np.random.normal(loc=0, scale=1, size=1000)

# 저첨도: uniform distribution
data_low = np.random.uniform(low=-3, high=3, size=1000)

# 첨도 출력
print("High kurtosis:", kurtosis(data_high))
print("Normal kurtosis:", kurtosis(data_normal))
print("Low kurtosis:", kurtosis(data_low))

# 시각화
fig, axes = plt.subplots(1, 3, figsize=(18, 5))

sns.histplot(data_high, bins=30, kde=True, color='orange', ax=axes[0])
axes[0].set_title("High Kurtosis")
axes[0].set_xlabel("Value")
axes[0].set_ylabel("Density")
axes[0].grid(True)

sns.histplot(data_normal, bins=30, kde=True, color='lightgreen', ax=axes[1])
axes[1].set_title("Normal Kurtosis")
axes[1].set_xlabel("Value")
axes[1].set_ylabel("Density")
axes[1].grid(True)

sns.histplot(data_low, bins=30, kde=True, color='skyblue', ax=axes[2])
axes[2].set_title("Low Kurtosis")
axes[2].set_xlabel("Value")
axes[2].set_ylabel("Density")
axes[2].grid(True)

plt.tight_layout()
plt.show()

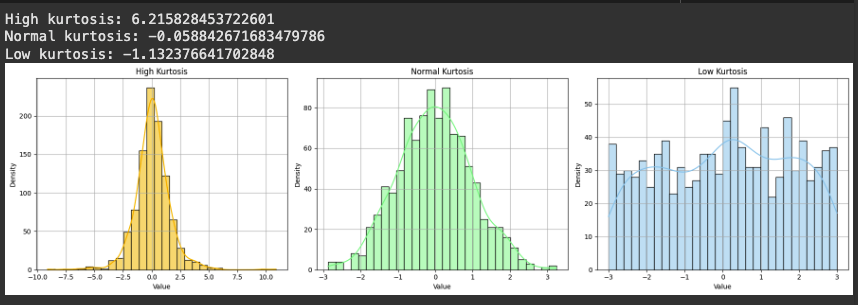
고첨도 분포에서 극단값(이상치) 자주 발생할 수 있음 > 예측 모델의 안정성에 영향을 줌
저첨도 분포는 데이터가 고르게 퍼져있어 중심 경향성만 보는 분석 한계 존재
첨도는 데이터의 위험성, 분포 특성, 모델 적합성을 평가할 때 중요한 지표가 됨

Comment Read more

통계 - 범위, 분산, 표준편차, 사분위수

04 Aug 2025 | Statistics

개인공부 후 자료를 남기기 위한 목적임으로 내용 상에 오류가 있을 수 있습니다.

범위(Range)

데이터 중 가장 큰 값과 가장 작은 값의 차이

데이터가 얼마나 퍼져있는지(흩어져 있는 지)를 확인하는 가장 단순한 방법

범위 = 최댓값 - 최솟값

delivery_days = [2, 1, 3, 2, 4, 1, 5]

max_val = max(delivery_days)
min_val = min(delivery_days)
range_val = max_val - min_val

print("최댓값:", max_val)  # 5
print("최솟값:", min_val)  # 1
print("범위:", range_val)  # 4

범위는 계산이 매우 간단하며 전체 데이터의 퍼짐 정도를 빠르게 알수 있다는 장점이 있지만, 극단적인 값(이상치)에 매우 민감하다. 대부분의 값이 비슷해도 한두개의 극단 값 때문에 범위가 크게 부풀려질 수 있고 이러한 데이터들 중간에 어떤 값들이 어떻게 분포되어 있는지는 알수 없다는 단점이 있다.

delivery_days_outlier = [2, 1, 3, 2, 4, 1, 30]  # 마지막 값이 이상치

range_outlier = max(delivery_days_outlier) - min(delivery_days_outlier)
print("이상치 포함 범위:", range_outlier)  # 30 - 1 > 29

분산(Variance)

데이터들이 평균으로부터 얼마나 떨어져있는 지를 나타내는 값

데이터 전체가 평균 근처에 몰려있는지, 아니면 흩어져 있는지를 수치로 표현
산포도를 측정하는 가장 기본적이고 중요한 지표

계산 방법

각 데이터에서 평균을 뺀다.
- → 얼마나 떨어져 있는지 확인
그 차이를 제곱한다.
- → 음수 제거 및 큰 차이에 더 민감하게
제곱한 값들의 평균을 구한다.

[\sigma^2 = \frac{1}{n} \sum_{i=1}^{n} (x_i - \bar{x})^2]

$\bar{x}$: 평균
$x_i$: i번째 데이터 값
$n$: 데이터의 개수

data = [30, 40, 20, 50, 60]

# 평균 계산
mean_val = sum(data) / len(data)

# 분산 계산
squared_diffs = [(x - mean_val)**2 for x in data]
variance = sum(squared_diffs) / len(data)

print("평균:", mean_val)  # 40.0
print("분산:", variance)  # 200.0

분산은 데이터의 전체적인 퍼짐 정도를 수치로 나타낼 수 잇으며, 평균을 중심으로 얼마나 퍼져있는지(변동이 있는지)를 나타낼 수 있다. 그러나 단위가 원래 데이터보다 커지고(제곱), 해석이 직관적이지 않다는 단점이 존재한다. 이 문제점때문에 ‘표준편차’라는 개념이 등장하게 된다.

표준편차(Standard Deviation)

분산의 제곱근

데이터를 평균 기준으로 얼마나 흩어져 있는지를 원래 단위로 해석할 수 있게 해주는 값
분산은 단위를 제곱해서 해석이 어렵지만
표준편차는 다시 제곱근을 씌우므로 실제 데이터 단위와 동일한 해석이 가능

[\sigma = \sqrt{ \frac{1}{n} \sum_{i=1}^{n} (x_i - \bar{x})^2 }]

$\sigma$: 표준편차
$x_i$: i번째 데이터
$\bar{x}$: 평균
$n$: 데이터 개수

import math

data = [30, 40, 20, 50, 60]

# 평균
mean_val = sum(data) / len(data)

# 분산
squared_diffs = [(x - mean_val)**2 for x in data]
variance = sum(squared_diffs) / len(data)

# 표준편차
std_dev = math.sqrt(variance)

print("분산:", variance)  # 200.0
print("표준편차:", std_dev)  # 14.142135623730951
# 40에서 약 ±14 떨어져 있다는 의미 
# 데이터의 흩어짐 정도(산포)를 실제 단위로 보여주는 값

표준편차의 의미

표준편차가 작다 > 대부분의 데이터가 평균근처에 모여있다
표준편차가 크다 > 대부분의 데이터가 평균으로부터 많이 흩어져 있다

이러한 표준편차는 단위가 원래 데이터와 같아서 해석이 직관적이며, 실제 통계분석에서도 널리 사용된다는 장점이 있다. 하지만 이러한 표준편차도 평균과 마찬가지로 극단값에 예민하며, 모든 데이터와 평균간의 거리 계산이 필요해 계산 비용이 존재한다는 단점도 존재한다.

사분위수와 IQR(Interquartile Range)

사분위수

데이터를 작은값부터 큰 값까지 정렬한 후, 이를 4등분한 위치에 있는 값을 의미

기호	이름	설명
Q1	제1사분위수	하위 25% 지점 (데이터의 25%가 이 값보다 작음)
Q2	제2사분위수	중앙값 (50% 지점)
Q3	제3사분위수	상위 25% 경계 (데이터의 75%가 이 값보다 작음)

IQR

사분위범위 데이터의 중간 50%가 어느범위에 분포해 있는지를 나타냄

[\text{IQR} = Q3 - Q1]

극단값(이상치)의 영향을 받지않고 데이터의 중간분포 폭을 파악할 수 있다.

data = [2, 4, 5, 6, 9, 10, 10, 12, 14]
data.sort()

n = len(data)

# Q2: 중앙값
if n % 2 == 1:
    q2 = data[n // 2]
else:
    q2 = (data[n//2 - 1] + data[n//2]) / 2

# Q1
lower_half = data[:n//2]
q1 = (lower_half[len(lower_half)//2 - 1] + lower_half[len(lower_half)//2]) / 2

# Q3
upper_half = data[(n+1)//2:]
q3 = (upper_half[len(upper_half)//2 - 1] + upper_half[len(upper_half)//2]) / 2

iqr = q3 - q1

print("Q1:", q1)  # 4.5
print("Q2 (중앙값):", q2)  # 9
print("Q3:", q3)  # 11.0
print("IQR:", iqr)  # 6.5

IQR은 이상치에 강하고 데이터의 중심 구간의 폭을 잘 설명해줄 수 있다. 그러나 평균이나 표준편차처럼 전체 데이터를 모두 반영하지는 않고, 정규분포에서 설명력이 다소 떨어질 수 있다는 단점이 존재한다.

구분	정의	계산 방식	장점	단점	이상치 영향
범위	최댓값과 최솟값의 차이	$\text{최댓값} - \text{최솟값}$	계산이 간단함	중간값이나 분포 형태는 반영하지 못함	매우 큼
분산	각 값이 평균에서 얼마나 떨어졌는지의 평균	$\frac{1}{n} \sum (x_i - \bar{x})^2$	전체 데이터의 흩어짐을 정량적으로 파악 가능	단위가 제곱이라 직관성이 낮음	큼
표준편차	분산의 제곱근	$\sqrt{ \frac{1}{n} \sum (x_i - \bar{x})^2 }$	분산보다 해석이 쉬움 (단위 동일)	이상치에 취약함	큼
IQR	중앙 50% 데이터 범위	$Q3 - Q1$	이상치의 영향을 거의 받지 않음, 데이터 중심 설명 가능	전체 데이터를 다 반영하지 않음	작음

요약 정리

빠르게 퍼짐 정도를 보고 싶을 땐 범위
전체 흩어짐을 정확히 측정하고 싶을 땐 분산이나 표준편차
이상치가 있을 가능성이 높다면 IQR을 사용하는 것이 좋다

Comment Read more

통계 - 평균, 중앙값, 최빈값

02 Aug 2025 | Statistics

개인공부 후 자료를 남기기 위한 목적임으로 내용 상에 오류가 있을 수 있습니다.

평균(Mean)

모든 값의 합을 전체 개수로 나눈 값

[\bar{x} = \frac{1}{n} \sum_{i=1}^{n} x_i]

$\bar{x}$: 평균 (x-bar라고 읽음)
$n$: 데이터의 개수 (전체 항목 수)
$x_i$: i번째 데이터 값
$\sum$: 시그마 기호, 모든 데이터를 더하라는 뜻

#A반 점수 모음
A_score = [60, 70, 90, 85, 100, 75, 65, 80, 95, 55 ]

#A반 합
a_sum = sum(A_score)

#A반 평균
a_sum/len(A_score)  # 77.5

평균은 계산이 쉽고 직관적이어서 데이터를 대표할 수 있는 값으로 많이 사용되지만, 어떤 특정한 극단적인 값에 영향을 받이 받는다는 단점도 존재한다.

중앙값(Median)

데이터를 크기순으로 정렬할때, 중앙에 위치한 값

# 원본 데이터
data1 = [30, 10, 20]

# 정렬
sorted_data1 = sorted(data1)  # [10, 20, 30]

# 중앙값 (홀수 개수)
n1 = len(sorted_data1)
median1 = sorted_data1[n1 // 2]

print("정렬된 데이터:", sorted_data1)
print("중앙값:", median1)

# [10, 20, 30]
# 20

그러나 데이터가 홀수개인 경우는 어떻게 할까?

# 원본 데이터
data2 = [40, 20, 10, 30]

# 정렬
sorted_data2 = sorted(data2)  # [10, 20, 30, 40]

# 중앙값 (짝수 개수 → 가운데 두 수의 평균)
n2 = len(sorted_data2)
middle_left = sorted_data2[n2 // 2 - 1]
middle_right = sorted_data2[n2 // 2]
median2 = (middle_left + middle_right) / 2

print("정렬된 데이터:", sorted_data2)
print("중앙값 계산:", middle_left, "+", middle_right, "/ 2 =", median2)
# [10, 20, 30, 40]
# 25.0

[\text{중앙값} = \frac{20 + 30}{2} = 25]

이러한 중앙값은 극단값(이상치)의 영향을 거의 받지 않고, 데이터가 한쪽으로 너무 치우쳐 있거나 이상치가 있을 경우 평균보다 더 현실적인 대표값을 가질 수 있다는 장점이 있다. 그러나 계산에 정렬이 반드시 필요하기 때문에 평균보다 더 많은 연산을 사용하게 되고, 모든 데이터 값을 반영하지 않고 단순히 위치만 고려한다는 단점 또한 존재한다.

따라서 데이터에 이상치가 존재하거나 분포가 비대칭인 경우 평균보다 중앙값을 대표값으로 사용하는 것이 적절하다.

최빈값(Mode)

데이터 중 가장 자주 나타나는 값 > 가장 많이 나온 값

fruits = ["사과", "바나나", "사과", "포도", "사과", "딸기", "바나나"]

freq = {}  # 빈 딕셔너리 

for fruit in fruits:
    if fruit in freq:
        # freq안에 과일 이미 존재하면 +1
        freq[fruit] += 1
    else:
        # freq안에 과일 없으면 1
        freq[fruit] = 1

# 결과 > freq = {'사과': 3, '바나나': 2, '포도': 1, '딸기': 1}

max_count = 0
mode_fruit = None

for key in freq:
    # 1. 사과(3)가 0보다 크면
    if freq[key] > max_count:
        # max_count = 3
        max_count = freq[key]
        # mode_fruit = 사과
        mode_fruit = key
# 사과(3) -> max_count 보다 큰 값은 안나올테니 
print("최빈값:", mode_fruit)
# 사과 

라이브러리를 통해서도 최빈값을 찾아보자

from collections import Counter

fruits = ["사과", "바나나", "사과", "포도", "사과", "딸기", "바나나"]
counter = Counter(fruits)
most_common = counter.most_common(1)[0][0]  # 가장 많이 등장한 값

print("최빈값:", most_common)
# 사과 

이러한 최빈값은 데이터에서 가장 흔하게 나타나는 값을 파악하기가 쉽다. 하지만 최빈값이 존재하지 않는 경우가 있을수도 있고(모든값이 한번만 나오는 경우), 여러개의 최빈값이 존재할 수도 있다는 것을 알고 있어야한다.

대표값 정리 비교

항목	의미	이상치 영향	적합한 데이터
평균	전체 합 ÷ 개수	있음	수치형 데이터
중앙값	정렬 후 가운데 위치	적음	비대칭 분포
최빈값	가장 자주 나타나는 값	없음	범주형 또는 수치형

Comment Read more

크롤링한 데이터 데이터프레임으로 만들어보기

31 Jul 2025 | DA

개인공부 후 자료를 남기기 위한 목적임으로 내용 상에 오류가 있을 수 있습니다.

beautifulSoup 사용

(정말 몇년만에 사용해보는..뷰티풀 숲인지 모르겠다.)

웹 크롤링을 굉장히 편리하게 할 수 있는 라이브러리이다. response.text를 통해 가져온 html 문서를 탐색해 원하는 부분을 뽑아내는 역학을 도와준다.

pip install beautifulsoup4

사용해보기(명언)

명언 홈페이지

from bs4 import beautifulsoup
import requests 

url = 'https://quotes.toscrape.com/'
# url로부터 요청을 받아 reponse에 담음 
response = requests.get(url)

# response에 들어온 html 텍스트를 파싱
soup = BeautifulSoup(response.text, 'html.parser')
# div 태그이면서 class 명이 quote인 모든 친구들을 찾음
quote_div = soup.find_all('div', class_='quote')

for quote_data in quote_div:
    # span태그이면서 class 명이 text인 에들의 텍스트 
    quote_text = quote_data.find('span', class_='text').text
    quote_author = quote_data('small', class_='author').text
    # a 태그안의 href
    quote_url = quote_data('a').get('href')

# 혹은 
quote_text = soup.select('div.quote>span.text')
quote_text_list = [i.text for i in quote_text]

quote_author = soup.select('div.quote>small.author')
quote_author_list = [i.text for i in quote_author]

find와 select의 차이

find: 내가 찾을 html 태그를 직접 입력
- soup.find_all(‘div’, class_=’quote’)
select: css 선택자를 통해 html 태그를 찾음
- soup.select(‘div.quote>span.text’)

데이터프레임으로 만들어보기

from bs4 import beautifulsoup
import requests 

url = 'https://quotes.toscrape.com/'
response = requests.get(url)

soup = BeautifulSoup(response.text, 'html.parser')
quote_div = soup.find_all('div', class_='quote')

text_list = []
author_list = []
url_list = []

for quote_data in quote_div:
    quote_text = quote_data.find('span', class_='text').text
    text_list.append(quote_text)
    quote_author = quote_data.find('small', class_='author').text
    text_list.append(quote_author)
    quote_url = quote_data.find('a').get('href')
    text_list.append(quote_url)

import pandas as pd

pd.DataFrame({
    'text': text_list, 
    'author': author_list,
    'url': url_list
})

테이블 데이터를 크롤링해보기

import pandas as pd

url = 'https://en.wikipedia.org/wiki/List_of_countries_by_stock_market_capitalization'
table_data = pd.read_html(url)

table_data[0]
table_data[0].head()  # 이렇게도 가능하다 

이때 table_data안에는 각 테이블들의 데이터가 리스트 안에 들어가 있기 때문에 인덱스틀 통해 테이블 데이터를 가져와서 쓸 수 있다.

Comment Read more

Pandas 데이터 전처리해보기(예시)

30 Jul 2025 | DA

개인공부 후 자료를 남기기 위한 목적임으로 내용 상에 오류가 있을 수 있습니다.

데이터 전처리

# 실제 지저분한 데이터
raw_data = {
    'customer_id': [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 2, 11, 12],  # 중복 있음
    'name': ['김철수', '이영희', '박민수', '최지은', None, '정다은', 'HONG GIL DONG', '김 철 수', '이영희', '신짱구', '이영희', '김영수', ''],
    'age': ['25', '30세', '35', 'Unknown', '28', '32', '45', '25', '30', '150', '30', '40', '25'],  # 다양한 형태
    'email': ['kim@gmail.com', 'lee@naver.com', 'park@', 'choi@gmail.com', None, 'jung@daum.net', 'hong@yahoo.com', 'kim2@gmail.com', 'lee@naver.com', 'shin@gmail.com', 'lee@naver.com', 'kim3@gmail.com', 'invalid_email'],
    'purchase_amount': ['100,000원', '$200', '150000', 'N/A', '80,000', '120000원', '300,000', '100000', '$200', '999999', '$200', '180000', '50,000원'],
    'join_date': ['2023-01-15', '23/02/20', '2023년 3월 10일', '2023-04-01', '2023/05/15', '20230615', 'Invalid', '2023-01-15', '2023/02/20', '2023-07-01', '2023/02/20', '2023-08-15', '2023-09-01'],
    'city': ['서울', 'Seoul', '부산', '대구', None, '인천', '서울시', '서울', '서울', '화성시', 'Seoul', '부산광역시', '대전']
}

df = pd.DataFrame(raw_data)
df

customer_id를 기준으로 중복 데이터 제거해보기

df.drop_duplicates(subset=['customer_id'], inplace=True)

나이 관련 전반적인 전처리

# 나이가 0-100사이면 그 숫자를 넣고, 아니면 np.nan
df['age'] = df['age'].where(df['age'].between(0,100), np.nan)
# 문자 '세' 없애기
df['age'].replace('세', '', regex=True, inplace=True)
# 알수없는 데이터에 np.nan
df['age'].replace(['Unknown','150'], np.nan, inplace=True)
# 문자형인 나이 모두 숫자로 변환 / errors='coerce' > 에러나는 애들은 그대로 
df['age'] = pd.to_numeric(df['age'], errors='coerce').astype('Int64')

이메일 관련 전반적인 전처리

정규표현식을 사용해 전처리 해보자

reg = r'^[a-zA-Z0-9._%+-]+@[a-zA-Z0-9.-]+.[a-zA-Z]{2,}$'
df['email'] = df['email'].where(df['email'].str.match(reg, na=False))

구매금액 관련 전반적인 전처리

# 위에서 중복관련된 데이터 삭제함으로써 어지러워진 인덱스 재 정렬
df.reset_index(drop=True, inplace=True)
# 양옆의 공백 제거
df['purchase_amount'].str.strip()

for i in range(len(df)):  # df의 컬럼 개수만큼 돌면서 (0~11)
    # purchase_amount 문자형 데이터만 amount 에 대입된다 
    amount = str(df.loc[i,'purchase_amount'])

    # amount가 str 타입인데, 한글자씩 순회중에 $가 있는게 있다면 
    if '$' in amount:
        # $ 제거
        clean = amount.replace('$', '')
        # 환율 계산하면서 purchase_amount에 데이터를 대입 
        df.loc[i, 'purchase_amount'] = int(clean)*1391
    else:
        # 남은 데이터들의 전처리 
        clean = amount.replace(',','').replace('원', '')

        # 이상치 혹은 NaN 친구들 처리 
        if clean in ['NaN', 'N/A', 'nan', '999999', '<NA>']:
            # 원래 NaN 이런애들은 실제 None 타입으로 있어야함(str이면 안됨)
            df.loc[i, 'purchase_amount'] = np.nan
        else:
            # 모두 int형으로 변환 
            df.loc[i, 'purchase_amount'] = int(clean)

이름 관련 전반적인 전처리

위 코드처럼 이름관련 데이터 전처리를 해봤다.

for i in range(len(df)):
    amount = df.loc[i, 'city']

    if amount in ['NaN', 'N/A', 'nan', '999999', '<NA>', None]:
        df.loc[i, 'city'] = np.nan
    else: 
        df['city'] = df['city'].replace(df.loc[i, 'city'], df.loc[i, 'city'][:2])
    
    if amount == 'Se':
        df['city'] = df['city'].replace('Se', '서울')

날짜 관련 전반적인 전처리

dateutil.parser 라이브러리를 사용했다. (설치는 할필요 없다)

일반적인 시간/날짜 포멧으로 파싱이 가능한 시간/날짜 스트링 파서를 제공

def safe_parse_date(x):
    try:
        # 컬럼에 널값이 있으면 
        if pd.isna(x): 
            # 그대로 널값을 두고 
            return pd.NaT
        # 없는경우, 들어온 스트링값을 형식에 맞게끔 변환 
        return parse(str(x), fuzzy=True)
    except Exception:
        return np.nan  # 변환 불가능한 값은 NaT로 처리

df['join_date'] = df['join_date'].apply(safe_parse_date)

Comment Read more

Older Newer

지혜의 개발공부로그

통계 - 분포, 정규분포, 왜도, 첨도

분포

왜 분포를 봐야 하는가?

정규분포(Normal Distribution)

정규분포의 특징

정규분포의 확률 분포 규칙 (68-95-99.7법칙)

정규분포가 중요한 이유

왜도(Skewness)

왜도의 종류

첨도(Kurtosis)

첨도의 종류

통계 - 범위, 분산, 표준편차, 사분위수

범위(Range)

분산(Variance)

계산 방법

표준편차(Standard Deviation)

표준편차의 의미

사분위수와 IQR(Interquartile Range)

사분위수

IQR

요약 정리

통계 - 평균, 중앙값, 최빈값

평균(Mean)

중앙값(Median)

최빈값(Mode)

대표값 정리 비교

크롤링한 데이터 데이터프레임으로 만들어보기

beautifulSoup 사용

사용해보기(명언)

데이터프레임으로 만들어보기

테이블 데이터를 크롤링해보기

Pandas 데이터 전처리해보기(예시)

데이터 전처리

customer_id를 기준으로 중복 데이터 제거해보기

나이 관련 전반적인 전처리

이메일 관련 전반적인 전처리

구매금액 관련 전반적인 전처리

이름 관련 전반적인 전처리

날짜 관련 전반적인 전처리