아노바(ANOVA)검정이란?
05 Aug 2025 | Statistics개인공부 후 자료를 남기기 위한 목적임으로 내용 상에 오류가 있을 수 있습니다.
데이터에 따른 분류
입력(x) - 출력(y)
- 수치 - 수치: 회귀모델
- 수치 - 범주(이진): 로지스틱회귀모델
- 범주 - 수치: t test, ANOVA
-
범주 - 범주: 카이제곱검정
모수적/비모수적
- 모수적: 데이터가 정규분포를 따름
- 비모수적: 정규분포에 대한 가정이 거의 없음 > 설명력이 떨어짐
ANOVA
| 구분 | 설명 |
|---|---|
| 목적 | 세 그룹 이상에서 평균 차이가 통계적으로 유의한지 검정 |
| 핵심 아이디어 | 그룹 간 분산(변동)과 그룹 내 분산(오차)을 비교해 F-통계량 도출 |
| 대표 예시 | ① 세 가지 학습법의 시험 점수 비교 ② 여러 공정 라인의 제품 수율 비교 |
두 그룹만 비교한다면 t-test가 적합하지만, 여러 그룹을 t-test로 반복하면 1종 오류(α)가 급격히 늘어난다 → ANOVA로 한 번에 검정!
기본 가정
- 독립성 : 각 관측치는 서로 독립
- 정규성 : 각 그룹의 데이터 분포가 정규
- 등분산성 : 각 그룹의 분산이 동일
가정이 심하게 깨질 때는 Kruskal-Wallis 같은 비모수 검정이나 Welch-ANOVA(등분산 가정 완화)를 고려한다.
예시
# 데이터 로딩
ris_data = load_iris()
df = pd.DataFrame(iris_data.data, columns=iris_data.feature_names)
df['species'] = iris_data.target_names[iris_data.target]
print("데이터셋 기본 정보:")
print(f"샘플 수: {len(df)}")
print(f"변수 수: {len(df.columns)-1}")
print(f"품종: {df['species'].unique()}")
# 데이터셋 기본 정보:
# 샘플 수: 150
# 변수 수: 4
# 품종: ['setosa' 'versicolor' 'virginica']
df
# 측정 변수들의 짧은 이름 정의
measurements = ['sepal length (cm)', 'sepal width (cm)',
'petal length (cm)', 'petal width (cm)']
short_names = ['꽃받침 길이', '꽃받침 폭', '꽃잎 길이', '꽃잎 폭']
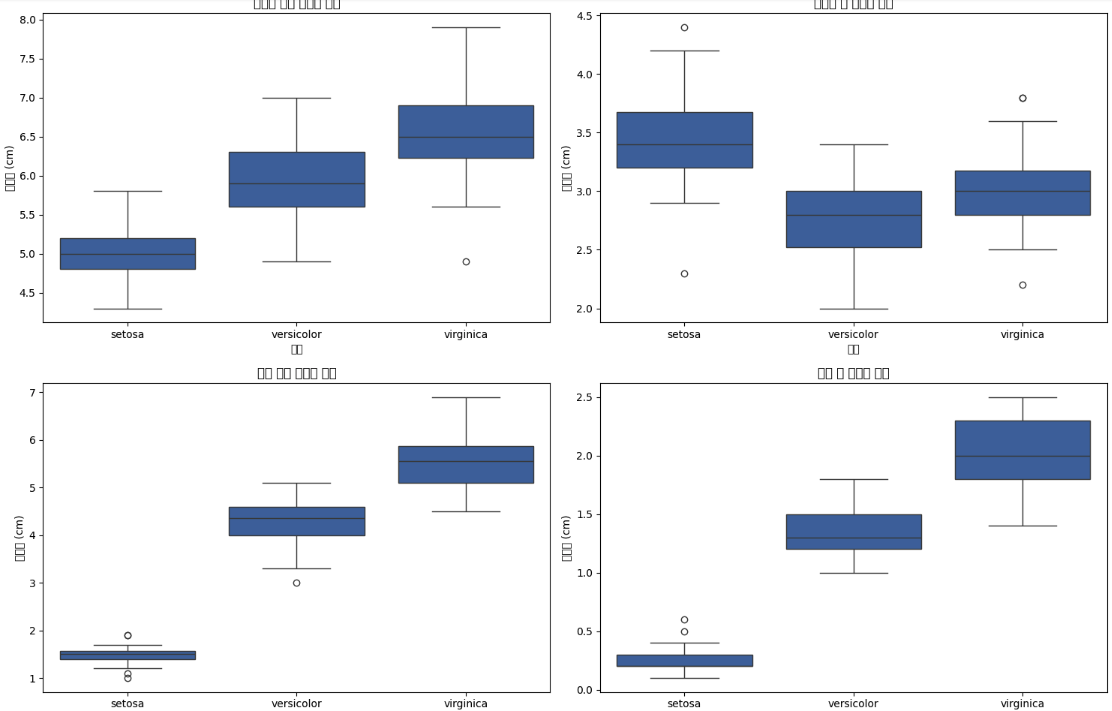
# 2x2 서브플롯으로 박스플롯 생성
fig, axes = plt.subplots(2, 2, figsize=(15, 10))
axes = axes.ravel()
for i, (measure, name) in enumerate(zip(measurements, short_names)):
sns.boxplot(data=df, x='species', y=measure, ax=axes[i])
axes[i].set_title(f'{name} 품종별 분포')
axes[i].set_xlabel('품종')
axes[i].set_ylabel('측정값 (cm)')
plt.tight_layout()
plt.show()
독립성 검정
실제 데이터테이블을 보고 데이터들이 다른 영역에 침법하고 있는지를 확인
즉, 수집된 샘플이 다른 개체에 영향을 주면 안된다.
정규성 검정
- 샤피로-윌크 검정(Shapiro-Wilk Test)은 주어진 데이터 샘플이 정규분포(Normal Distribution)를 따르는지 확인하기 위한 통계적 검정 방법
print("=== 정규성 검정 (Shapiro-Wilk Test) ===")
print("H0: 데이터가 정규분포를 따른다")
print("p > 0.05이면 정규성 가정 충족\n")
for measure, name in zip(measurements, short_names):
print(f"[{name}]")
for species in df['species'].unique():
data = df[df['species'] == species][measure]
statistic, p_value = stats.shapiro(data)
result = "충족" if p_value > 0.05 else "위반"
print(f" {species}: p = {p_value:.4f} ({result})")
print()
=== 정규성 검정 (Shapiro-Wilk Test) ===
H0: 데이터가 정규분포를 따른다
p > 0.05이면 정규성 가정 충족
[꽃받침 길이]
setosa: p = 0.4595 (충족)
versicolor: p = 0.4647 (충족)
virginica: p = 0.2583 (충족)
[꽃받침 폭]
setosa: p = 0.2715 (충족)
versicolor: p = 0.3380 (충족)
virginica: p = 0.1809 (충족)
[꽃잎 길이]
setosa: p = 0.0548 (충족)
versicolor: p = 0.1585 (충족)
virginica: p = 0.1098 (충족)
[꽃잎 폭]
setosa: p = 0.0000 (위반)
versicolor: p = 0.0273 (위반)
virginica: p = 0.0870 (충족)
등분산성 가정 검토
- 레빈 검정(Levene Test)은 두 개 이상의 집단(group)들의 분산이 서로 같은지 확인하는 통계적 방법으로 이를 분산의 동질성(homogeneity of variance)이라 한다.
print("=== 등분산성 검정 (Levene Test) ===")
print("H0: 모든 집단의 분산이 같다")
print("p > 0.05이면 등분산성 가정 충족\n")
for measure, name in zip(measurements, short_names):
# 각 품종별 데이터 분리
setosa_data = df[df['species'] == 'setosa'][measure]
versicolor_data = df[df['species'] == 'versicolor'][measure]
virginica_data = df[df['species'] == 'virginica'][measure]
# Levene 검정
statistic, p_value = stats.levene(setosa_data, versicolor_data, virginica_data)
result = "충족" if p_value > 0.05 else "위반"
print(f"{name}: F = {statistic:.4f}, p = {p_value:.4f} ({result})")
=== 등분산성 검정 (Levene Test) ===
H0: 모든 집단의 분산이 같다
p > 0.05이면 등분산성 가정 충족
꽃받침 길이: F = 6.3527, p = 0.0023 (위반)
꽃받침 폭: F = 0.5902, p = 0.5555 (충족)
꽃잎 길이: F = 19.4803, p = 0.0000 (위반)
꽃잎 폭: F = 19.8924, p = 0.0000 (위반)
Anova 분석 > 변수 3개
f_stat, p_val = stats.f_oneway(setosa, versicolor, virginica)
print(f"F-통계량: {f_stat:.4f}")
print(f"p-value: {p_val}")
# F-통계량: 119.2645
# p-value: 1.6696691907693826e-31
일원분산 분석(One-way ANOVA)
import statsmodels.api as sm
from statsmodels.formula.api import ols
# 선형회귀 분석 ols
# Q("sepal length (cm)" 변수 하나를 넣고, 모델 훈련시키고
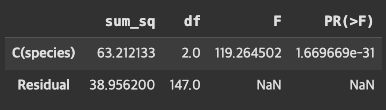
model = ols('Q("sepal length (cm)") ~ C(species)', data=df).fit()
# residual > 잔차를 계산한것, F > F 통계량 값
anova_table = sm.stats.anova_lm(model, typ=2)
anova_table
사후검정(Post-hoc test)
사후 검정은 분산분석(ANOVA)에서 “집단 간 차이가 있다”는 결과를 얻은 후, 구체적으로 어떤 집단들 사이에 유의미한 차이가 있는지 알아보기 위해 수행하는 추가 분석
from statsmodels.stats.multicomp import pairwise_tukeyhsd
turkey = pairwise_tukeyhsd(endog=df["sepal length (cm)"], groups=df["species"], alpha=0.05)
print(turkey)
Multiple Comparison of Means - Tukey HSD, FWER=0.05
=========================================================
group1 group2 meandiff p-adj lower upper reject
---------------------------------------------------------
setosa versicolor 0.93 0.0 0.6862 1.1738 True
setosa virginica 1.582 0.0 1.3382 1.8258 True
versicolor virginica 0.652 0.0 0.4082 0.8958 True
---------------------------------------------------------
- setosa > versicolor > virginica 순서대로 sepal length 차이가 크다
- reject: 귀무가설 기각 여부 / true면 기각
- 좀 더 객관적으로 파악하고 싶을때 사용

 지혜의 개발공부로그
지혜의 개발공부로그