지혜의 개발공부로그

머신러닝 - 결정트리(Decision Tree)

27 Aug 2025 | Machine Learning

개인공부 후 자료를 남기기 위한 목적임으로 내용 상에 오류가 있을 수 있습니다.

결정트리(Decision Tree)

의사결정트리는 분류와 같은 의사결정을 수행할 때, 나무와 같이 가지치기를 하면서 분류하는 방법이다. 이 결정트리는 분류와 회귀모델 모두 사용가능하지만, 회귀모델의 정확도는 낮기 때문에 주로 분류의 목적으로 사용된다.

규칙노드(decision node)로 표시된 노드는 규칙 조건이 담겨져 있고, 리프노드(lead node)로 표시된 노드는 결정된 클래스 값, 즉 지니가 0이 되어 더이상 분할이 필요없는 말단노드를 의미한다. 그리고 새로운 규칙조건마다 서브트리(sub tree)가 형성되는데 데이터 셋에 피쳐(feature -> y)가 있고, 이 피처가 결합해 규칙 조건마다 서브트리가 생성되는 것이다.

하지만 많은 규칙이 있다는 것은 곧 분류를 결정하는 방식이 더욱 복잡해진다는 뜻으로 과잡합이 되기가 쉬워진다. 그렇기 떄문에 트리의 깊이(depth)가 깊어질수록 결정트리의 예측 성능이 저하될 가능성이 높아진다.

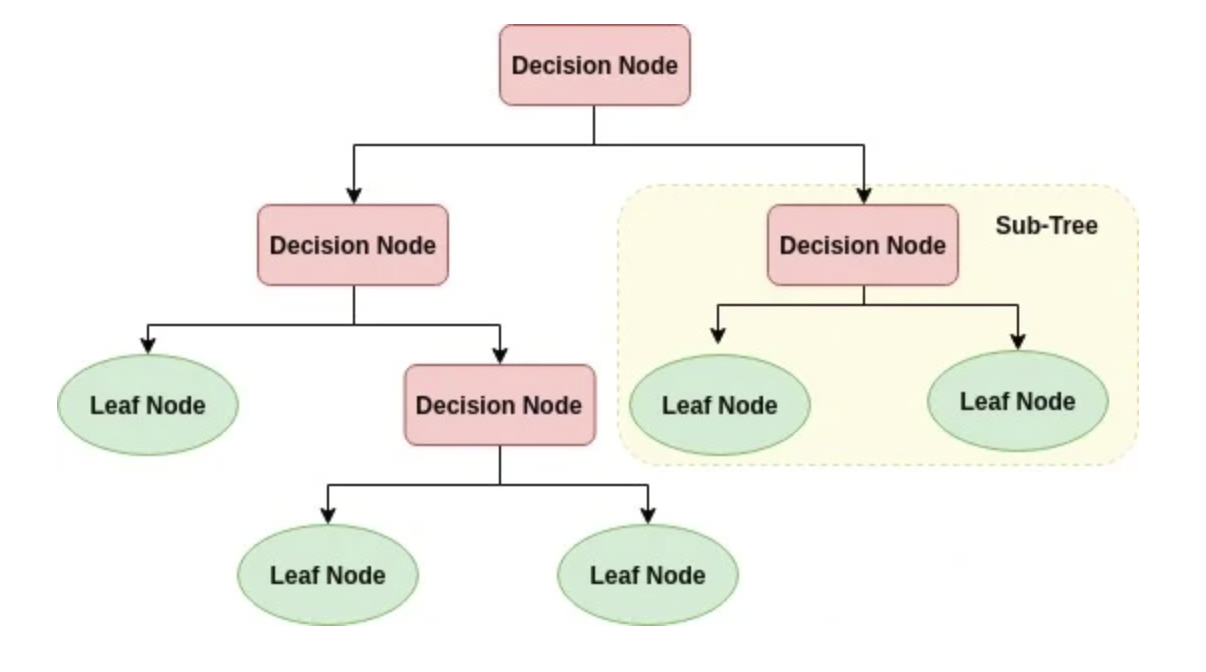
가능한한 적은 결정 노드로 높은 예측 정확도를 가지기 위해서는 데이터를 분류할 때, 최대한 많은 데이터 셋이 해당 분류에 속할 수 있도록 결정 노드의 규칙이 정해져야 한다. 즉 결정노드의 규칙이 굉장이 중요한 것을 의미한다.

이를 위해서는 트리를 분할(split)할 것인가가 중요한데, 최대한 균일한 데이터 셋을 구성할 수 있도록 분할하는 것이 굉장히 중요하다.

결정노드는 정보 균일도가 높은 데이터 셋을 먼저 선택할 수 있도록 규칙조건을 만드는데, 이 정보의 균일도를 측정하는 대표적인 방법이 엔트로피를 이용한 정보이득지수와 지니계수인 것이다.

지니불순도와 엔트로피

각 노드에서 판단하기 위한 두개의 기준은 다음과 같다. (의사결정트리가 데이터를 어떻게 분할할지 결정하는 역할)

  1. 지니불순도: 데이터의 불순도 혹은 혼잡도를 측정하는 지표
    • 지니불순도가 0 이상 1에 가까워질수록 불순도가 있다는 의미
    • 0이 되면 최고 순도로 더이상 분할이 필요없다는 것을 의미
    • 지니계수가 낮은 속성을 기준으로 분할
\[Gini = 1 - \sum_{j=1}^J p_j^2\]
  1. 엔트로피(정보이득지수): 데이터 분포의 순수도를 나타내는 척도(불확실성을 나타내는 지표)
    • 서로 다른 값(정보)이 많이 섞여 있으면 엔트로피가 높고, 같은 값(정보)가 섞여있으면 엔트로피가 낮음
    • 데이터의 순도가 높을수록 엔트로피 값은 낮아지고 불순도가 높을수록 엔트로피 값은 높아짐
    • 정보이득지수 = 1 - 엔트로피지수
    • 정보이득이 높은 속성을 기준으로 분할함
\[Entropy = - \sum_{j=1}^{J} p_j \log_2(p_j)\]

구성

  • 노드(node)
    • 뿌리마디(root node): 시작되는 마디
    • 자식마디(child node): 마디에서 분리된 2개 이상의 마디
    • 부모마디(parent node): 주어진 마디의 상위 마디
    • 끝마디(leaf node): 자식 마디가 없는 마디 > 최종클래스(레이블)값이 결정되는 노드
    • 중간마디(internal node): 부모, 자식마디 둘다 있는 마디
  • 가지(branch, edge): 선
  • 깊이(depth): 중간마디들의 수

특징

  • 장점
    • 정보의 균일도를 기반으로 하고있어 알고리즘이 쉽고 직관적임
    • 시각화로 표현 가능
    • 스케일링이나 정규화 같은 전처리 작업이 필요없음(정보의 균일함만 보면 됨)
  • 단점
    • 모든 데이터 상황을 만족하도록 트리 조건을 계속 추가하다보면 과적합이 발생함
    • 모든 데이터 상활을 만족할 필요는 없게 사전에 트리 크기를 제한하는 것이 필요
    • 즉 하이퍼파리미터를 통해 성능을 높여나가는 것이 중요!
criterion:
    - 분류 "gini"|"entropy"
    - 회귀 "squared_error"|"friedman_mse"|"absolute_error"

max_depth: 트리 최대 깊이(과적합 강력 제어)
min_samples_split: 분할 최소 샘플 수(노이즈 분할 억제)
min_samples_leaf: 리프 최소 샘플 수(일반화↑, 편향 약간↑)
max_features: 분할 시 고려할 특징 수(랜덤성 부여)
class_weight: 불균형 분류 가중치(예: `"balanced"`)
ccp_alpha: 비용-복잡도 가지치기 강도(0→성장, ↑→단순 트리)

실습

# 라이브러리 불러오기
import pandas as pd
import numpy as np

from sklearn.datasets import load_iris #아이리스 데이터
from sklearn.model_selection import train_test_split #데이터 분리
from sklearn.tree import DecisionTreeClassifier, plot_tree # 단일 트리모델, 트리그림 확인
import matplotlib.pyplot as plt # 시각화

# 데이터 불러오기
iris = load_iris()
X = iris.data
y = iris.target

# 데이터 분할
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)

# 트리모델 정의 > Clissifier 단일트리모델 분류모델
# max_depth가 작다? = 분류가 잘 안됨 / max_depth가 너무 많다? = 과적합, 의사결정 잘 안됨
# 적절한 max_depth를 하는 것이 중요
clf = DecisionTreeClassifier(random_state=42, max_depth=3, criterion='gini')

# 모델 훈련
clf.fit(X_train, y_train)

# 정확도 확인
clf.score(X_train, y_train)
# 0.9666666666666667

clf.score(X_test, y_test)
# 0.9333333333333333

이때 마지막 두 값을 비교해 모델 성능이 괜찮은지 아닌지를 판단해야한다.

현재 결과는 train이 test 결과보다 정확도가 더 높은 것을 볼 수 있다. > 오버피팅

이때 이 과적합이란, 모델이 학습(train) 데이터에만 과도하게 최적화되어 실제 예측을 다른 데이터로 수행할 경우 예측 성능이 떨어지는 경우를 의미한다.

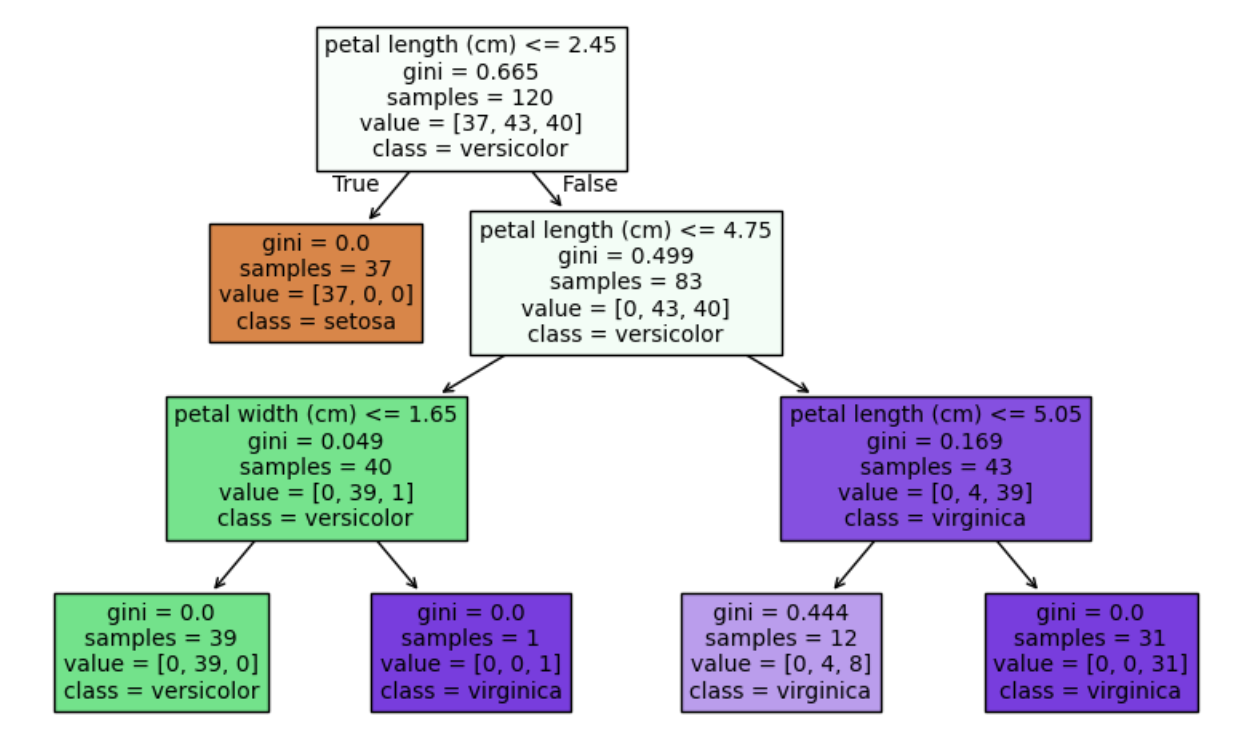
# 시각화
plt.figure(figsize=(10,6))
plot_tree(clf, feature_names=iris.feature_names, class_names=iris.target_names, filled=True)
plt.show()

Related Posts