지혜의 개발공부로그

머신러닝 - 실습 문제풀이(덴드로그램, K-Means) & 거리측정 방법 비교

27 Aug 2025 | Machine Learning

개인공부 후 자료를 남기기 위한 목적임으로 내용 상에 오류가 있을 수 있습니다.

K-Means 와인데이터 클러스터링(군집화)

# 라이브러리 불러오기 
from sklearn.datasets import load_wine
from sklearn.preprocessing import StandardScaler
from sklearn.cluster import KMeans
from sklearn.metrics import adjusted_rand_score
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt

# 데이터 불러오기
data = load_wine()
X = data.data

# 데이터 전처리(> 정규화)
X_scaled = StandardScaler().fit_transform(X)

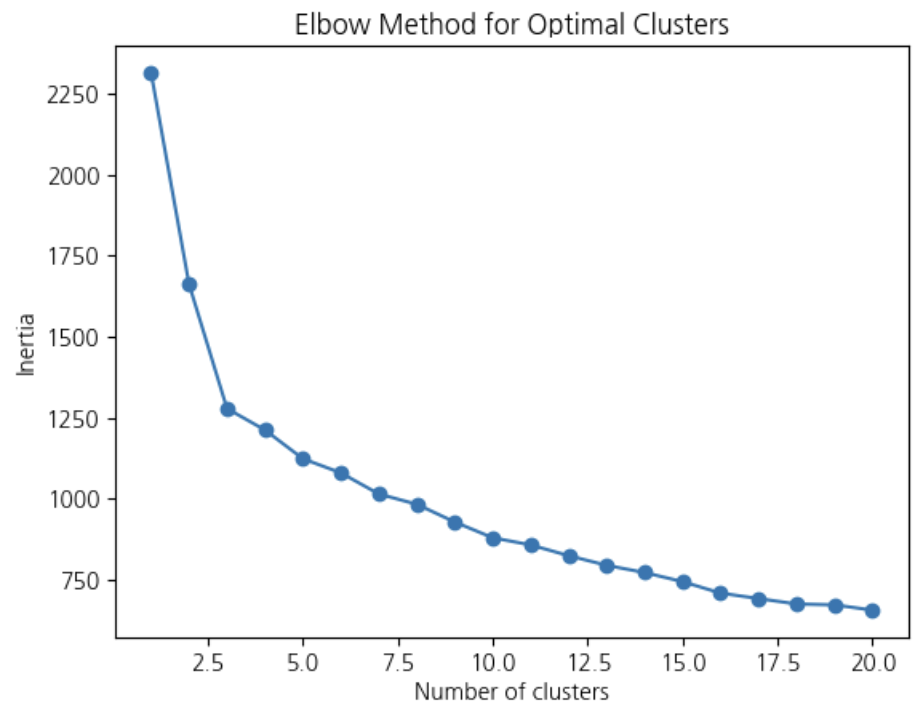
# 최적의 클러스터 수 찾기 > 엘보우 방법으로 클러스터 수를 1~20까지 설정 
# 각 경우의 inertia값을 구하기 > 이를 엘보우 그래프를 통해 최적의 클러스터 수 정하기 
inertia = []
K_range = range(1, 21)

# for문 돌면서 거리합을 구함
for k in K_range:
    kmeans = KMeans(n_clusters=k, random_state=42)
    kmeans.fit(X_scaled)
    inertia.append(kmeans.inertia_)

plt.plot(K_range, inertia, marker='o')
plt.title('Elbow Method for Optimal Clusters')
plt.xlabel('Number of clusters')
plt.ylabel('Inertia')
plt.show()

# kmeans 클러스터링
kmeans = KMeans(n_clusters=3, random_state=42)
kmeans.fit(X_scaled)
# 각 클러스터의 레이블 저장 
kmeans_labels = kmeans.labels_

# 클러스터링 성능평가 > adjusted_rand_score
y = data.target
print("Adjusted Rand Index:", adjusted_rand_score(y, kmeans_labels))

# 결과 시각화 
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X_scaled)

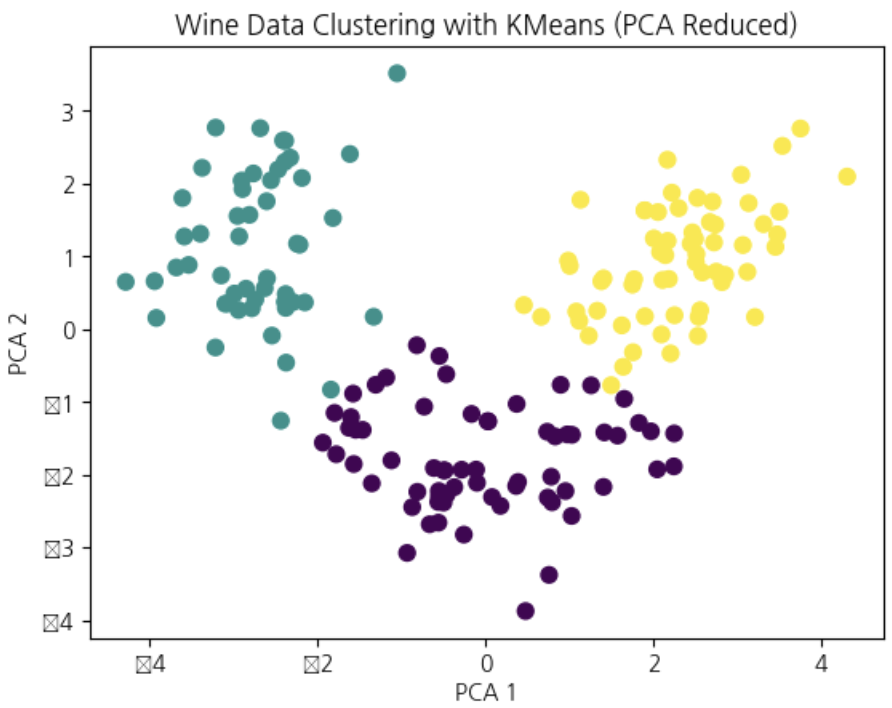
plt.scatter(X_pca[:, 0], X_pca[:, 1], c=kmeans_labels, cmap='viridis', s=50)
plt.title('Wine Data Clustering with KMeans (PCA Reduced)')
plt.xlabel('PCA 1')
plt.ylabel('PCA 2')
plt.show()

덴드로그램

# 라이브러리 불러오기 
import numpy as np
import matplotlib.pyplot as plt
from scipy.cluster.hierarchy import dendrogram, linkage #   덴드로그램 라이브러리
from sklearn.datasets import make_blobs

# 데이터 불러오기
X, _ = make_blobs(n_samples=30, centers=4, n_features=2,
                  random_state=42, cluster_std=1.5)

# 거리측정 > ward 방식으로
linkage = linkage(X, method='ward')

# 덴드로그램 시각화 
plt.figure(figsize=(12, 8))
dendrogram(linkage, leaf_rotation=90, leaf_font_size=10)
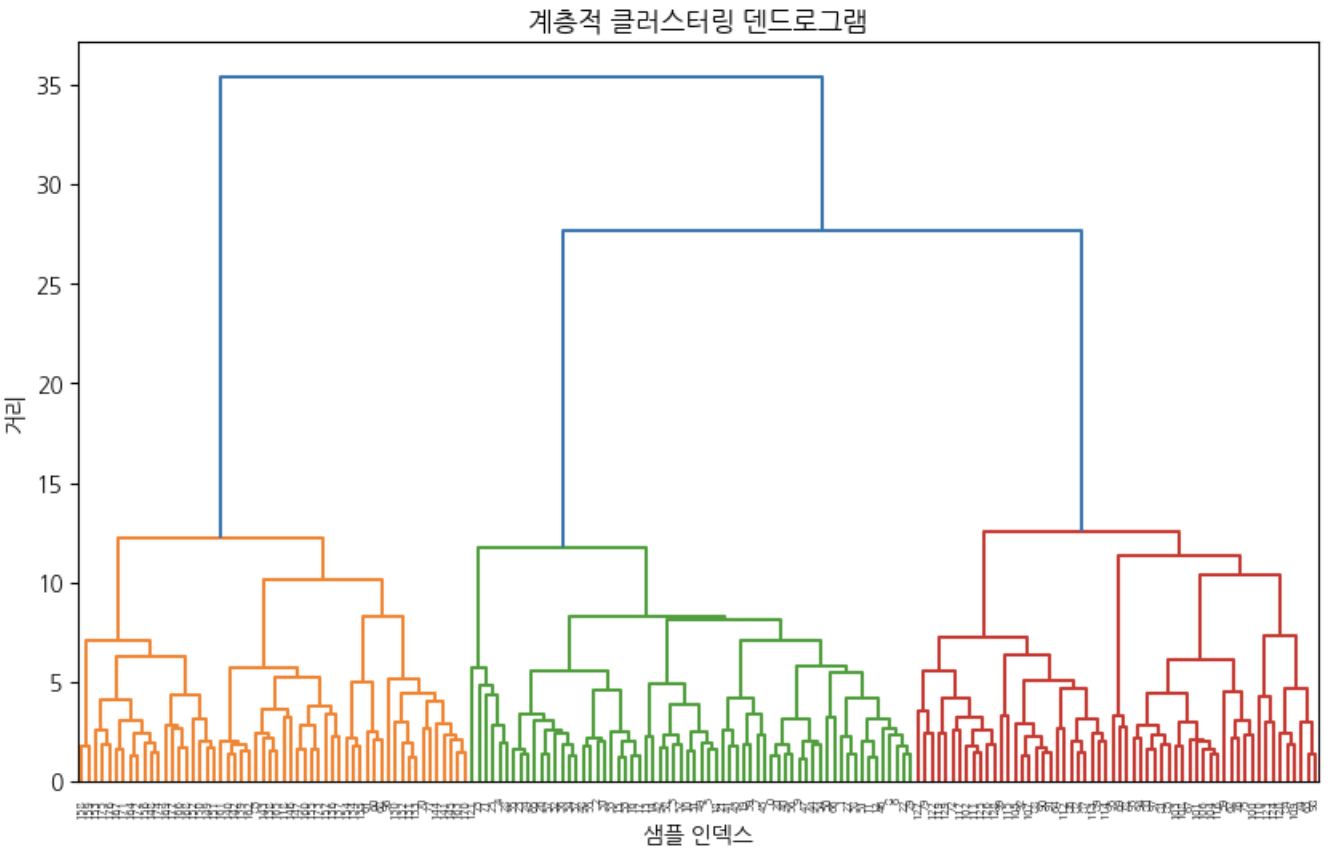
plt.title('계층적 클러스터링 덴드로그램')
plt.xlabel('샘플 인덱스')
plt.ylabel('거리')
plt.show()

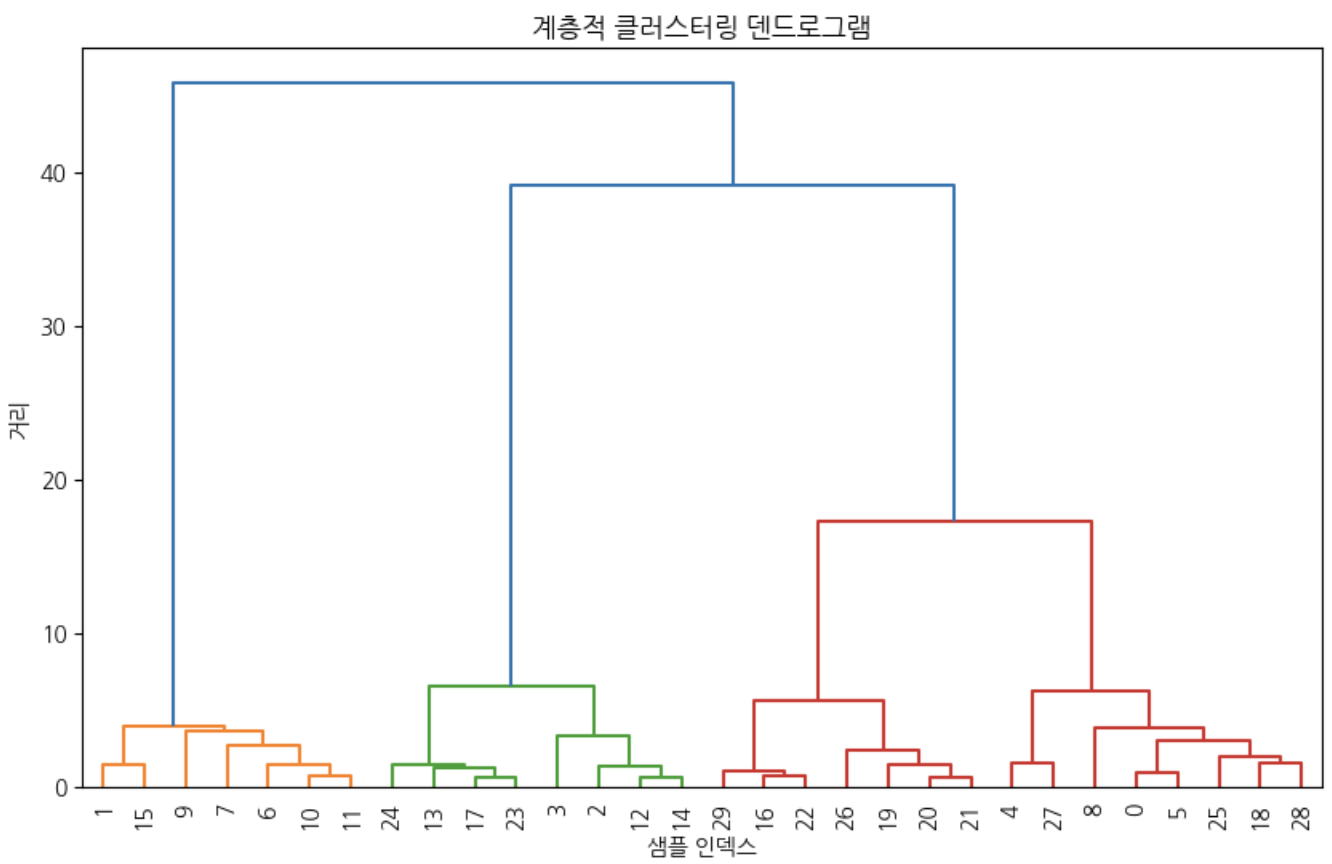
이때 사후적으로 클러스터를 어떻게 나눌 것인지에 대한 고민이 필요하다.

from sklearn.cluster import AgglomerativeClustering
from sklearn.decomposition import PCA

# 3개 할 것이라고 지정
optimal_clusters = 3
# 예측하고
hierarchical = AgglomerativeClustering(n_clusters=optimal_clusters, linkage='ward')
hierarchical_labels = hierarchical.fit_predict(X)

# 이를 pca로 넣어준다
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X)

plt.scatter(X_pca[:, 0], X_pca[:, 1], c=hierarchical_labels, cmap='viridis', s=50)
plt.title('Wine Data Clustering with Hierarchical Clustering (PCA Reduced)')
plt.xlabel('PCA 1')
plt.ylabel('PCA 2')
plt.show()

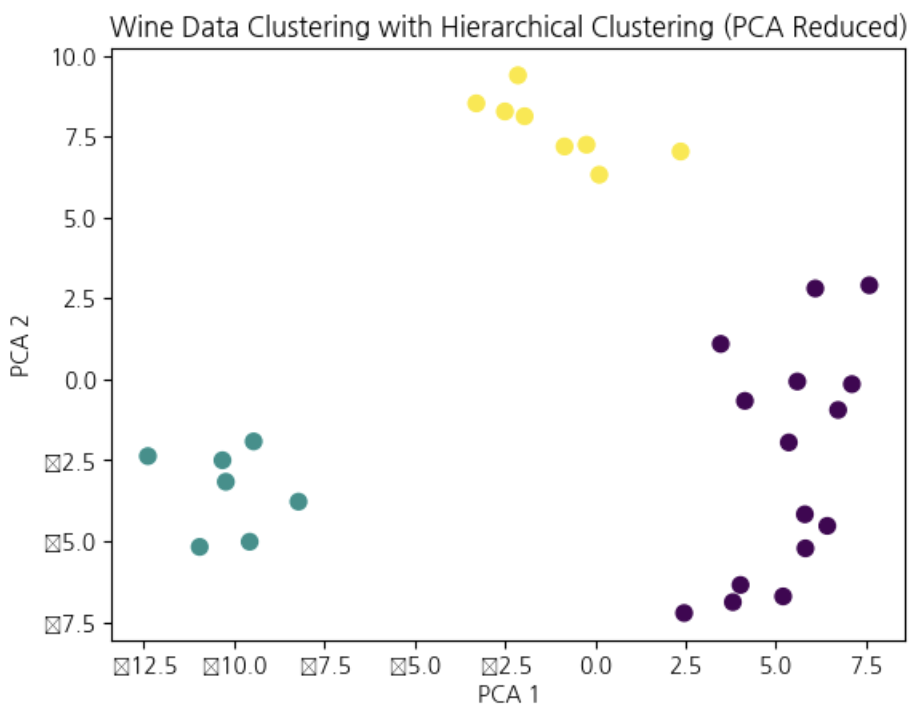
shc를 이용해 와인데이터 계층적 클러스터링 진행해보기

# 라이브러리 불러오기 
from sklearn.datasets import load_wine
import numpy as np
import matplotlib.pyplot as plt
from scipy.cluster.hierarchy import dendrogram, linkage  #덴드로그램 라이브러리
from sklearn.datasets import make_blobs

import scipy.cluster.hierarchy as shc

# 데이터 불러오기
data = load_wine()
X = data.data
y = data.target

# 데이터 전처리 (> 정규화)
X_scaled = StandardScaler().fit_transform(X)

# 덴드로그램 그리기 
plt.figure(figsize=(12, 8))
shc.dendrogram(shc.linkage(X_scaled, method='ward'))
plt.title('계층적 클러스터링 덴드로그램')
plt.xlabel('샘플 인덱스')
plt.ylabel('거리')
plt.show()

# 계층적 클러스터링
hierarchical_labels = AgglomerativeClustering(n_clusters=3, linkage='ward').fit_predict(X_scaled)

# 클러스터링 성능 평가
print("Adjusted Rand Index:", adjusted_rand_score(y, hierarchical_labels))

# 결과 시각화 
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X_scaled)

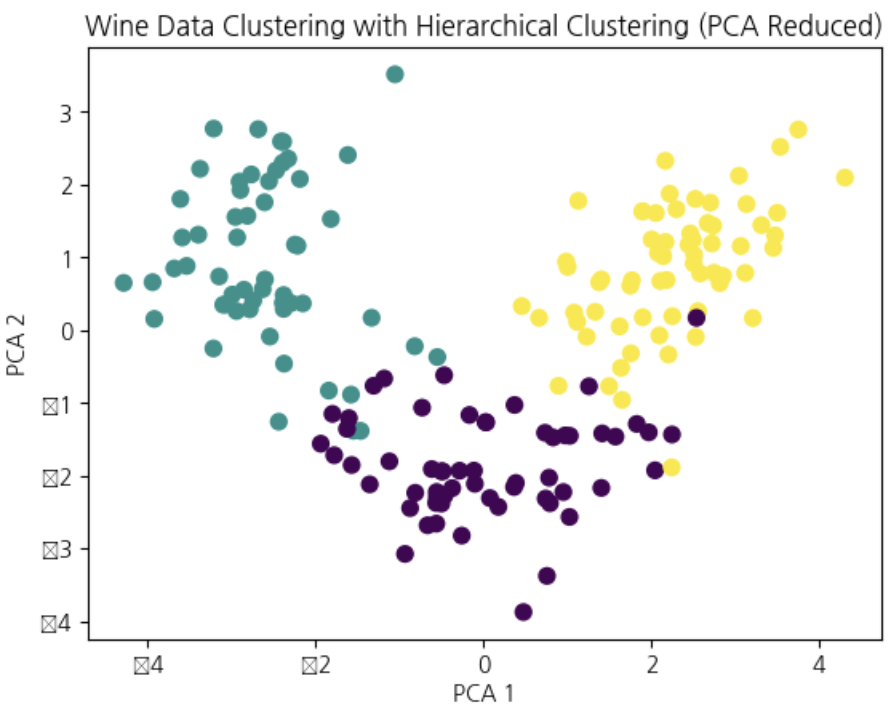
plt.scatter(X_pca[:, 0], X_pca[:, 1], c=hierarchical_labels, cmap='viridis', s=50)
plt.title('Wine Data Clustering with Hierarchical Clustering (PCA Reduced)')
plt.xlabel('PCA 1')
plt.ylabel('PCA 2')
plt.show()

Adjusted Rand Score (ARS)

Adjusted Rand Score는 두 클러스터링 결과의 유사도를 측정하며, 우연히 일치할 확률을 보정한 지표

ARS = (RI - Expected_RI) / (Max_RI - Expected_RI)

여기서:

  • RI: Rand Index
  • Expected_RI: 무작위 클러스터링의 기대값
  • Max_RI: 최대 가능한 Rand Index (=1)

거리 측정 방법 비교

1. Single Linkage (최단 연결법)

  • 두 클러스터 간의 최소 거리를 기준으로 정의
  • 두 클러스터 $A, B$ 사이 거리:
\[D_{\text{single}}(A, B) = \min_{x \in A, \, y \in B} d(x, y)\]
  • 가장 가까운 두 점을 연결하는 방식 → 체인(chain) 형태로 묶이는 경향이 있음

2. Complete Linkage (최장 연결법)

  • 두 클러스터 간의 최대 거리를 기준으로 정의
  • 두 클러스터 $A, B$ 사이 거리:
\[D_{\text{complete}}(A, B) = \max_{x \in A, \, y \in B} d(x, y)\]
  • 가장 먼 두 점을 기준으로 병합 → 구 모양의 클러스터를 잘 찾음

3. Average Linkage (평균 연결법, UPGMA)

  • 클러스터 간의 모든 점들 사이 거리의 평균을 사용
  • 두 클러스터 $A, B$ 사이 거리:
\[D_{\text{average}}(A, B) = \frac{1}{|A| \, |B|} \sum_{x \in A} \sum_{y \in B} d(x, y)\]
  • 전체적으로 균형 잡힌 클러스터를 찾는 데 유리

4. Ward’s Method (분산 최소화 방법)

  • 클러스터 병합 시, **클러스터 내 제곱합(Within-Cluster Variance, SSE)**의 증가량이 최소가 되도록 함.
  • 수식 (클러스터 $A, B$ 병합 시 비용):
\[D_{\text{ward}}(A, B) = \frac{|A| \, |B|}{|A| + |B|} \, \| \bar{x}_A - \bar{x}_B \|^2\]

여기서 $\bar{x}_A$ = 클러스터 $A$의 평균 벡터 $\bar{x}_B$ = 클러스터 $B$의 평균 벡터

  • 데이터 분산을 최소화하는 방향으로 군집화 진행

Related Posts