머신러닝 - 비지도학습(덴드로그램, K-Means)
26 Aug 2025 | Machine Learning개인공부 후 자료를 남기기 위한 목적임으로 내용 상에 오류가 있을 수 있습니다.
비지도 학습?
보유한 데이터에 타겟값(y)가 없는 경우
- 계층적 군집화 > 덴드로그램
- 비계층적 군집화 > K-Means, DBSCAN 등을 사용
비지도 학습은 서비스 단에서는 사용 불가능 & 서비스를 이해할 때만 사용 가능
높은 정확도를 가지기 힘들기 때문
덴드로그램
모델을 구동 후 사후적으로 군집을 나눌 수 있음
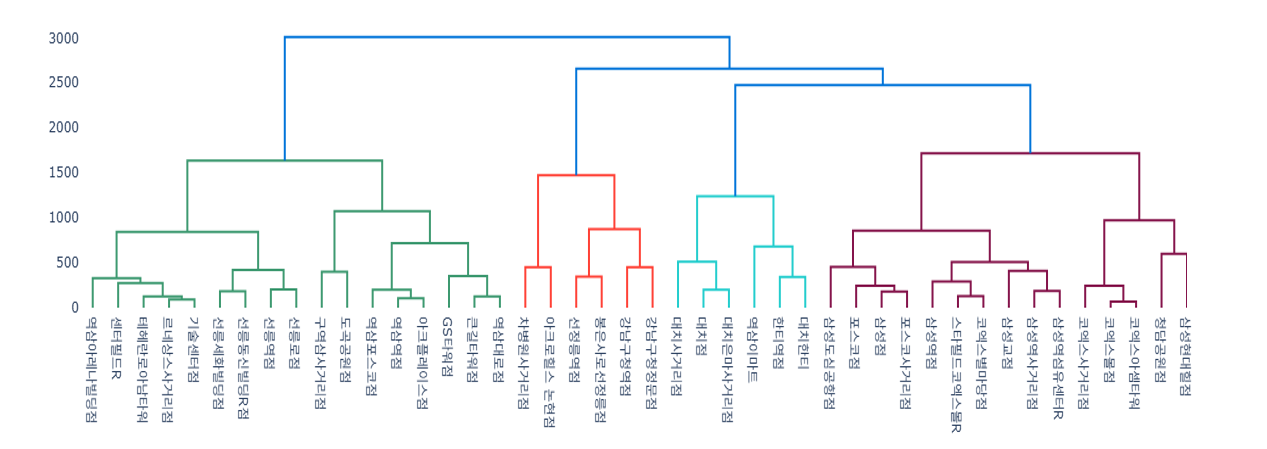
위 그림에서 내가 2000을 기준으로 군집을 나눈다면, 위에서 군집은 총 4개로 나뉘게 됨! (2000을 기준으로 가로 직선을 그어보면 됨)
하지만 이는 연산이 많아질 수 있고, 초반에 잘못 분류되면 오분류의 가능성이 있다는 단점이 존재함.
K-Means
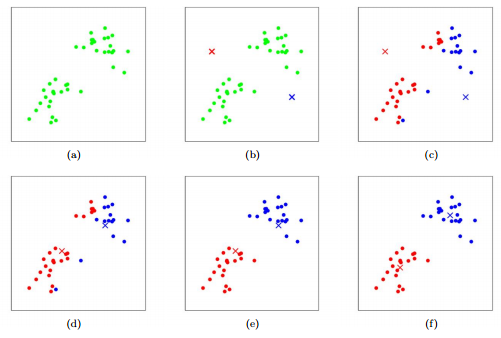
- 초반에 센트로이드 설정을 해주고,
- 센트로이드를 중심으로 거리를 계산함.
- 센트로이드가 거리를 최소화하는 방향으로 이동함
- 다시한번 나머지 애들끼리 이동하고
- 센트로이드가 거리 계산해서 이동.. 반복..
- 센트로이드 중심으로 이동하다보니, 연산이 덴드로그램보다는 적다.
- 그러나 군집이 몇개가 될지 알수가 없어서, 초반 센트로이드를 설정해야하는 것이 단점이다.
- 센트로이드가 적정 군집보다 크면 안좋으니까 > 왜곡된다고 보면 된다.
라이브러리 불러오기
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.cluster import KMeans
from sklearn.decomposition import PCA
데이터 불러오기
iris = load_iris()
X = iris.data
모델 정의
# n_clusters: 데이터의 센트로이드를 설정
# 센트로이드: 군집의 중심 > 그 중심을 내가 정해주는 것 > 몇개의 군집으로 설정할 것인지?
kmeans = KMeans(n_clusters=3, random_state=42)
모델 훈련
kmeans.fit(X)
cluster = kmeans.fit_predict(X)
시각화 > 주성분 분석(PCA)
labels = kmeans.labels_
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X)
centroids = pca.transform(kmeans.cluster_centers_)
plt.figure(figsize=(10, 7))
plt.scatter(X_pca[:, 0], X_pca[:, 1], c=labels, cmap='viridis', marker='o', edgecolor='k', s=50)
plt.scatter(centroids[:, 0], centroids[:, 1], c='red', marker='X', s=200, label='Centroids')
plt.title('K-Means Clustering on Iris Dataset')
plt.xlabel('PCA Component 1')
plt.ylabel('PCA Component 2')
plt.legend()
plt.show()
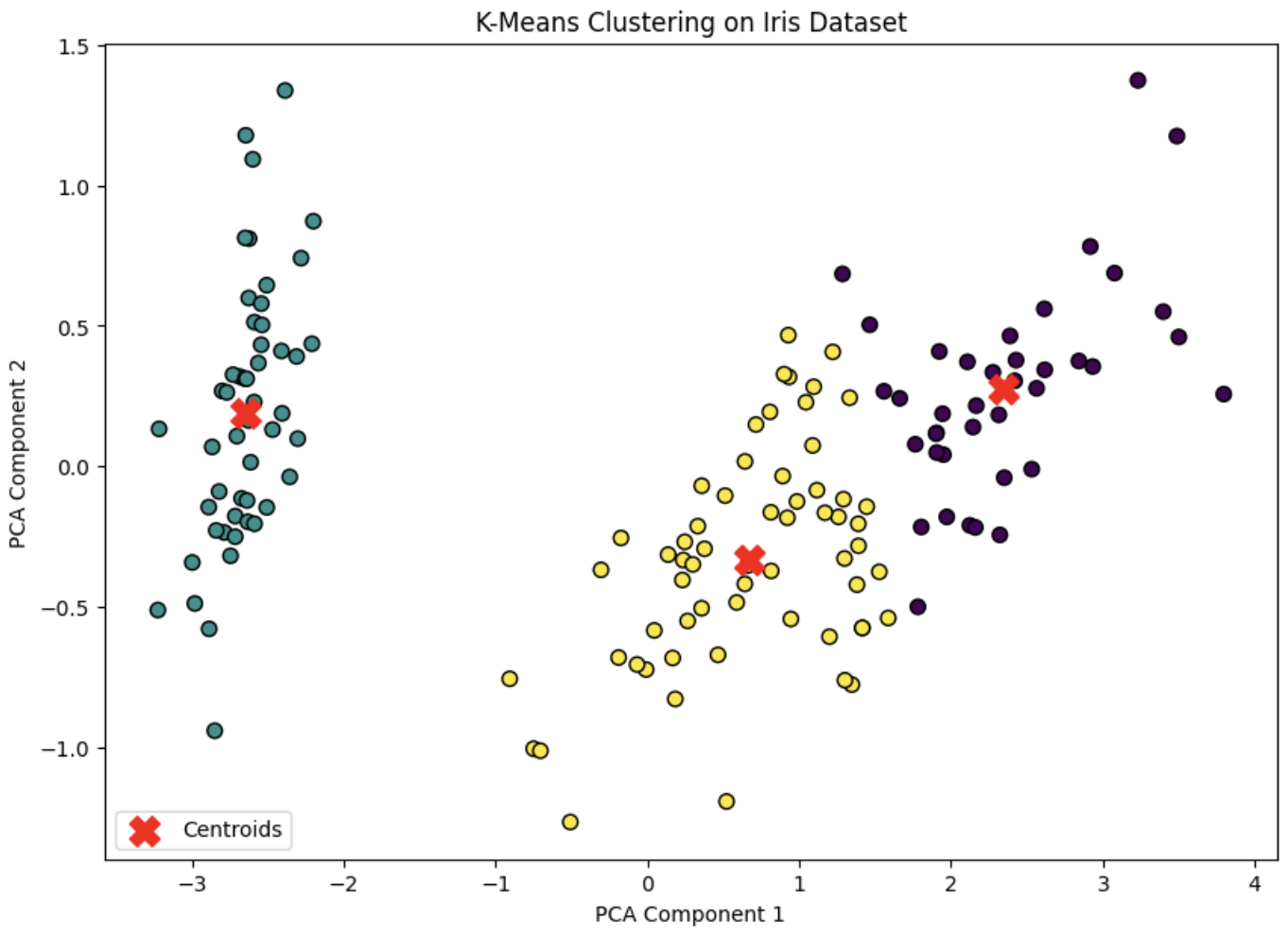
K-Means의 약점은 초반 센트로이드를 선택해야하는 것에 있는데, 이를 보완한 라이브러리로는
- 엘보우
- 실루엣 계수 가 있다. (적정 군집을 구하는 방법임)
- 엘보우: for문 돌면서 거리합을 구함, (클러스터 갯수가 증가했을떄 합이 최소화 되는 방향으로)
- 갯수마다의 증감 차이를 봐야하며 어느순간 덜 줄어드는 때를 봐줘야 함 > 최적의 군집을 찾는게 중요
- k가 증가하면 SSE(에러의 합)이 줄어드는 것을 보는 것으로 최적 k는 SSE 감소율이 급격히 줄어드는 팔꿈치 지점임
- 센트로이드와 점들의 거리를 에러 > 이 에러의 합을 줄이는게 목표
# 다양한 K값에 대해 성능 측정
inertias = []
K_range = range(1, 4)
# for문 돌면서 거리합을 구함
for k in K_range:
kmeans = KMeans(n_clusters=k, random_state=42)
kmeans.fit(X)
inertias.append(kmeans.inertia_)
# 엘보우 그래프 그리기
plt.figure(figsize=(8, 5))
plt.plot(K_range, inertias, 'bo-')
plt.xlabel('클러스터 개수 (K)')
plt.ylabel('Inertia (클러스터 내 거리의 합)')
plt.title('📈 최적의 K 찾기: Elbow Method')
plt.grid(True, alpha=0.3)
plt.show()
# 팔꿈치 부분이 최적의 K!
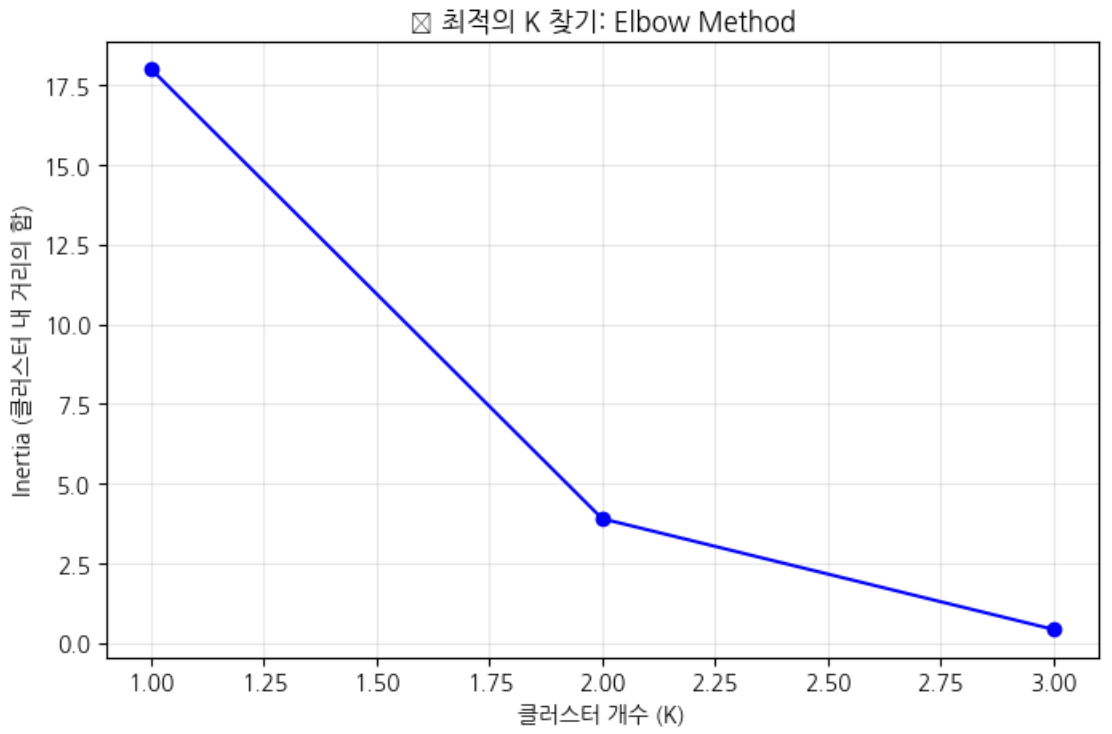
1개였을떄의 거리합과 2개였을때의 거리합이 확연히 줄어드는 것을 볼 수 있다.
- 실루엣: for문 돌면서 predict, predict에서 실루엣 한 것을 클러스터에 얼마나 잘 속해있는 지를 측정함
- 하나의 군집을 클러스터라고 하는데, 같은 클러스터 내 센트로이드와 다른 점들과의 거리를 재고 가장 가까운 다른 클러스터 까지의 평균거리를 가지고 계산식으로 실루엣 계수를 정함
- 실루엣 계수가 크면 적절(1에 가까우면)
- 음수는 이상치가 많이 껴있을 경우로 잘못된 클러스터에 할당된 것
- 0에 가까울수록 클러스터 경계에 위치한 것
from sklearn.metrics import silhouette_score
# 실루엣 점수 계산
silhouette_scores = []
K_range = range(2, 4) # 최소 2개 그룹 필요
for k in K_range:
kmeans = KMeans(n_clusters=k, random_state=42)
labels = kmeans.fit_predict(X)
score = silhouette_score(X, labels)
silhouette_scores.append(score)
print(f"K={k}: 실루엣 점수 = {score:.3f}")
# 가장 높은 점수가 최적의 K!
best_k = K_range[np.argmax(silhouette_scores)]
print(f"\n🎯 최적의 K: {best_k}")
실습해보기
data = {
'연간구매금액': [20, 25, 30, 100, 120, 110, 200, 250, 220],
'연간방문횟수': [5, 8, 6, 20, 25, 22, 40, 45, 38]
}
df = pd.DataFrame(data)
데이터 스케일링
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X = scaler.fit_transform(df)
K-Means
kmeans = KMeans(n_clusters=3, random_state=42)
# kmeans.fit(X)
# cluster_labels = kmeans.labels_
cluster_labels = kmeans.fit_predict(X)
결과 확인
df['고객그룹'] = cluster_labels
시각화
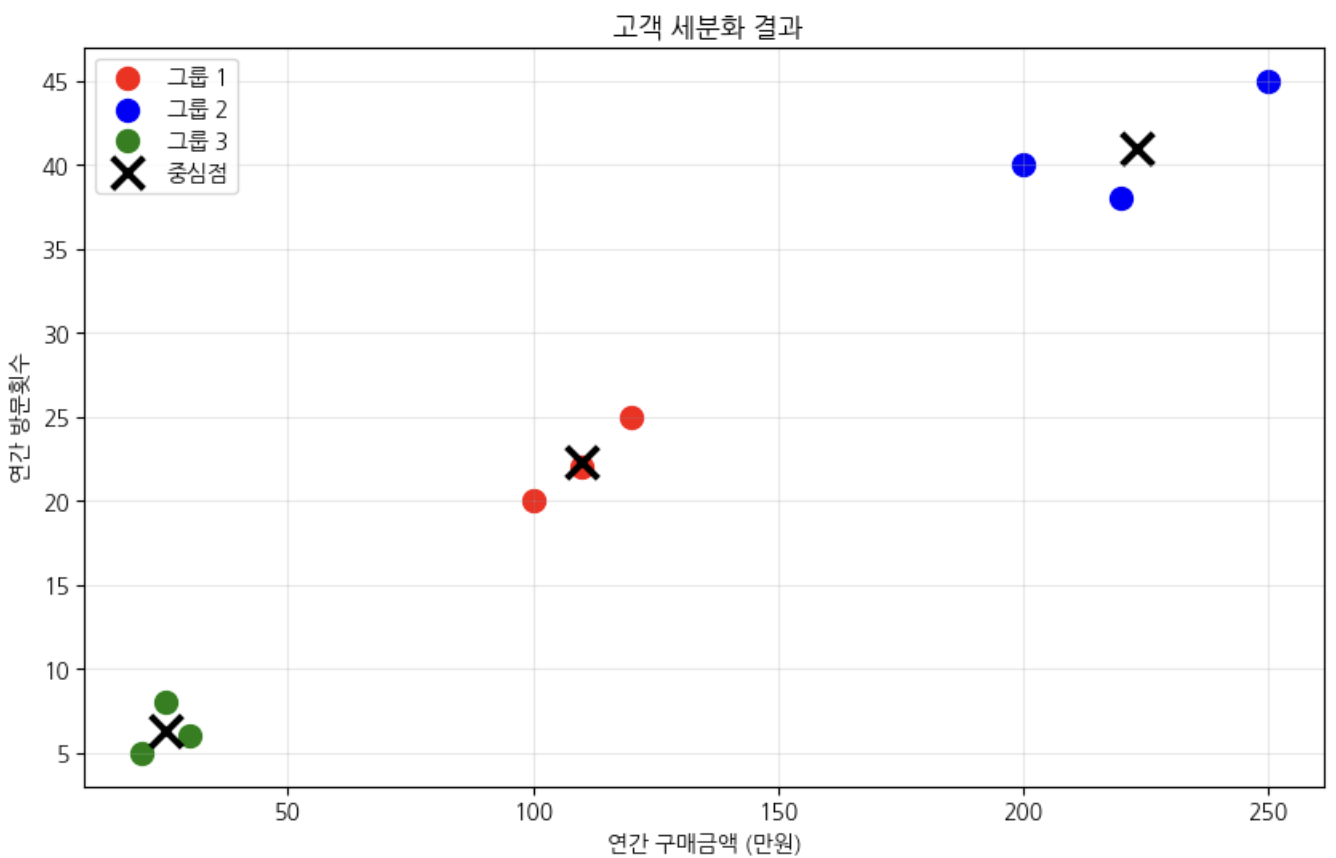
plt.figure(figsize=(10, 6))
colors = ['red', 'blue', 'green']
for i in range(3):
mask = cluster_labels == i
plt.scatter(df[mask]['연간구매금액'], df[mask]['연간방문횟수'],
c=colors[i], label=f'그룹 {i+1}', s=100)
# 중심점 표시
centers_original = scaler.inverse_transform(kmeans.cluster_centers_)
plt.scatter(centers_original[:, 0], centers_original[:, 1],
c='black', marker='x', s=200, linewidths=3, label='중심점')
plt.xlabel('연간 구매금액 (만원)')
plt.ylabel('연간 방문횟수')
plt.title(' 고객 세분화 결과')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()

 지혜의 개발공부로그
지혜의 개발공부로그