지혜의 개발공부로그

머신러닝 - 모델 정규화(Ridge, Lasso, Elastic Net)

26 Aug 2025 | Machine Learning

개인공부 후 자료를 남기기 위한 목적임으로 내용 상에 오류가 있을 수 있습니다.

정규화(Regularization)란?

머신러닝/딥러닝 학습에서의 정규화란 모델의 과적합을 막기위해, 모델 성능의 일반화를 위해 수행되는 것을 의미함

모델이 너무 복잡해지거나, 파라미터의 개수가 너무 많아지는 것을 막기 위해 정규화를 사용함. 이 대표적인 종류로 L1, L2 정규화가 있다.

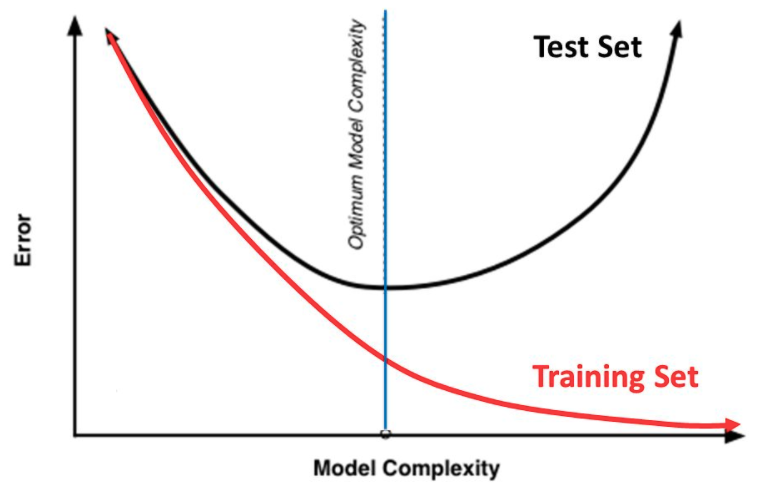
위 그림과 같이 정규화는 모델 복잡도, 정확도 면에서 최적의 해를 찾는 것이 정규화의 수행 의의이다.

릿지(Ridge) Regression > L2 규제

  • 릿지 회귀는 선형 회귀를 개선한 선형 모델
  • 릿지 회귀는 선형 회귀와 비슷하지만, 가중치의 절대값을 최대한 작게 만든다는 것이 다름
  • 이러한 방법은 각각의 특성(feature)이 출력 값에 주는 영향을 최소한으로 만들도록 규제(regularization)를 거는 것
  • 규제를 사용하면 다중공선성(multicollinearity) 문제를 방지하기 때문에 모델의 과대적합을 막을 수 있게 됨
  • 다중공선성 문제는 두 특성이 일치에 가까울 정도로 관련성(상관관계)이 높을 경우 발생
  • 릿지 회귀는 다음과 같은 함수를 최소화하는 파라미터 $w$를 찾음
\[\text{RidgeMSE} = \frac{1}{N} \sum_{i=1}^{N}(y_i - \hat{y}_i)^2 + \alpha \sum_{i=1}^{p} w_i^2\]
  • $\alpha$ : 사용자가 지정하는 매개변수
  • $\alpha$가 크면 규제의 효과가 커지고, $\alpha$가 작으면 규제의 효과가 작아짐

라이브러리 불러오기

from sklearn.linear_model import LinearRegression, Ridge, Lasso  # 선형회귀, 릿지, 랏쏘
from sklearn.model_selection import train_test_split  # 데이터셋 분리
from sklearn.metrics import mean_squared_error, r2_score  # matrixs MSE, r^2
import matplotlib.pyplot as plt  # 시각화 
import numpy as np
import pandas as pd

데이터 불러오기

df = pd.read_csv('https://ds-lecture-data.s3.ap-northeast-2.amazonaws.com/house-prices/house_prices_train.csv')

X = df[['GrLivArea', 'LotArea']]
y = df['SalePrice']

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

모델 정의

# 𝛼 가 크면 규제의 효과가 커지고,  𝛼 가 작으면 규제의 효과가 작아짐
ridge_model = Ridge(alpha=0.1)

ridge_model.fit(X_train, y_train)

모델 예측

pred_ridge = ridge_model.predict(X_test)  # X_test에 따른 predict 값이 나옴 

MSE_ridge = mean_squared_error(y_test, pred_ridge)
MSE_ridge
# 3389531220.090343

릿지(Lasso) Regression > L1 규제

  • 선형 회귀에 규제를 적용한 또 다른 모델로 라쏘 회귀가 있음
  • 라쏘 회귀는 릿지 회귀와 비슷하게 가중치를 0에 가깝게 만들지만, 조금 다른 방식을 사용
  • 라쏘 회귀에서는 다음과 같은 함수를 최소화하는 파라미터 $w$를 찾음
\[\text{LassoMSE} = \frac{1}{N} \sum_{i=1}^{N}(y_i - \hat{y}_i)^2 + \alpha \sum_{i=1}^{p}|w_i|\]
  • 라쏘 회귀도 매개변수인 $\alpha$ 값을 통해 규제의 강도 조절 가능

구현해보기

lasso_model = Lasso(alpha=0.3)
lasso_model.fit(X_train, y_train)

pred_lasso = lasso_model.predict(X_test)

MSE_lasso = mean_squared_error(y_test, pred_lasso)
MSE_lasso
# 3389531228.8286858

Elastic-Net(Ridge+Lasso)

  • 신축망은 릿지 회귀와 라쏘 회귀, 두 모델의 모든 규제를 사용하는 선형 모델
  • 두 모델의 장점을 모두 갖고 있기 때문에 좋은 성능을 보임
  • 데이터 특성이 많거나 서로 상관 관계가 높은 특성이 존재할 때 위의 두 모델보다 좋은 성능을 보여줌
  • 신축망은 다음과 같은 함수를 최소화하는 파라미터 $w$를 찾음
\[\text{ElasticMSE} = \frac{1}{N} \sum_{i=1}^{N}(y_i - \hat{y}_i) + \alpha \rho \sum_{i=1}^{p}|w_i| + \alpha(1-\rho) \sum_{i=1}^{p} w_i^2\]
  • $\alpha$ : 규제의 강도를 조절하는 매개변수
  • $\rho$ : 라쏘 규제와 릿지 규제 사이의 가중치를 조절하는 매개변수

구현해보기

from sklearn.linear_model import ElasticNet
# 엘라스틱 모델 정의
elastic_model = ElasticNet(alpha=0.3, l1_ratio=0.5)
# 엘라스틱 모델 훈련
elastic_model.fit(X_train, y_train)

# 예측
pred_elastic = elastic_model.predict(X_test)

# MSE 
MSE_elastic = mean_squared_error(y_test, pred_elastic)
MSE_elastic
# 3389531933.0839124

Related Posts