머신러닝 - 선형 회귀분석 모델(Linear Regression) 2
25 Aug 2025 | Machine Learning개인공부 후 자료를 남기기 위한 목적임으로 내용 상에 오류가 있을 수 있습니다.
실습해보기
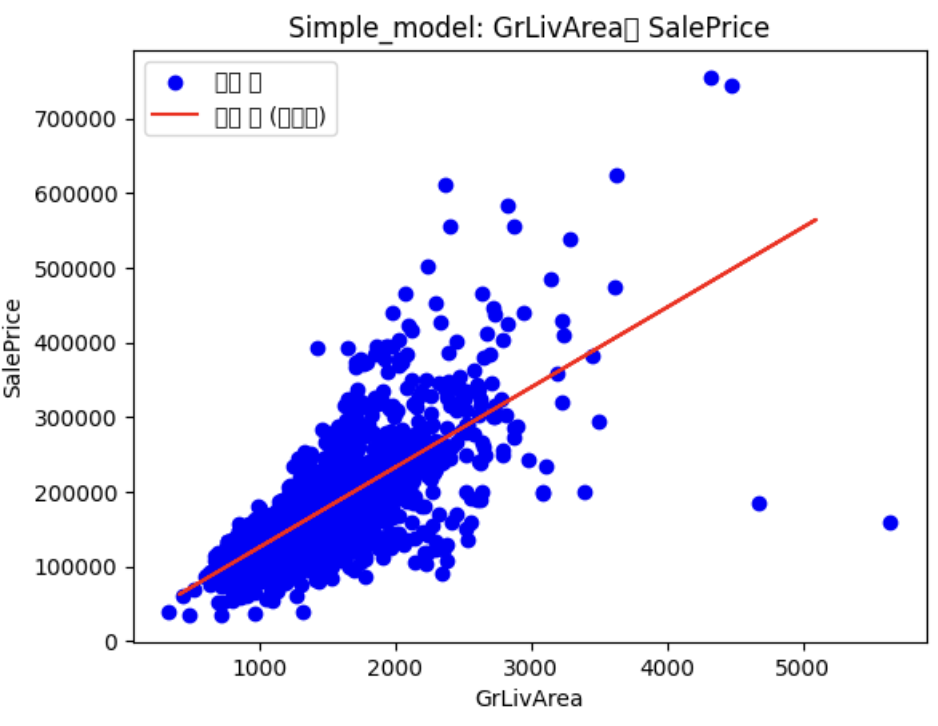
문제1(단순 선형회귀): GrLivArea 를 사용해서 SalePrice 예측하기
- 테스트 데이터와 훈련 데이터를 각각 위치에 넣고
- 학습시키고 & 성능지표 확인하기
# 라이브러리 불러오기
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
# 훈련 데이터
df = pd.read_csv('https://ds-lecture-data.s3.ap-northeast-2.amazonaws.com/house-prices/house_prices_train.csv')
# 테스트 데이터
df_t = pd.read_csv('https://ds-lecture-data.s3.ap-northeast-2.amazonaws.com/house-prices/house_prices_test.csv')
# 데이터 불러오기
X = df[['GrLivArea']]
y = df['SalePrice']
# 모델 정의
model = LinearRegression()
# 모델 훈련
model.fit(X,y)
# 모델 예측
X_t = df_t[['GrLivArea']]
y_pred = model.predict(X_t)
# 훈련 결과 확인
print(f"단순 회귀 - 기울기(GrLivArea): {model3.coef_[0]:.2f}")
print(f"단순 회귀 - 절편: {model3.intercept_:.2f}")
plt.scatter(X, y, color="blue", label="실제 값")
plt.plot(X_t, y_pred, color="red", label="예측 값 (회귀선)")
plt.xlabel("GrLivArea")
plt.ylabel("SalePrice")
plt.legend()
plt.title("Simple_model: GrLivArea와 SalePrice")
plt.show()
문제2(다중 선형회귀): GrLivArea와 LotArea를 사용해 SalePrice를 예측
# 데이터 불러오기
X = df[['GrLivArea', 'LotArea']]
y = df['SalePrice']
# 모델 정의
model4 = LinearRegression()
# 모델 훈련
model4.fit(X, y)
# 모델 예측
y_pred = model4.predict(X)
X_t = df_t[['GrLivArea','LotArea']]
y_pred_t = model4.predict(X_t) # 실제데이터가 아닌 테스트 데이터로 예측
MSE = mean_squared_error(y, y_pred)
MSE
# 3099258070.4722357
좋은 모델이란?
- Good Explanatory Model (좋은 설명 모델)
- 현재 데이터(트레이닝 데이터)를 잘 설명
- 트레이닝 에러가 작아야 함
- 최소제곱법(Least Squares)을 통해 MSE 최소화
- Good Predictive Model (좋은 예측 모델)
- 미래 데이터에 대한 예측 성능이 우수
- 테스트 에러가 작아야 함
- 일반화 성능이 중요
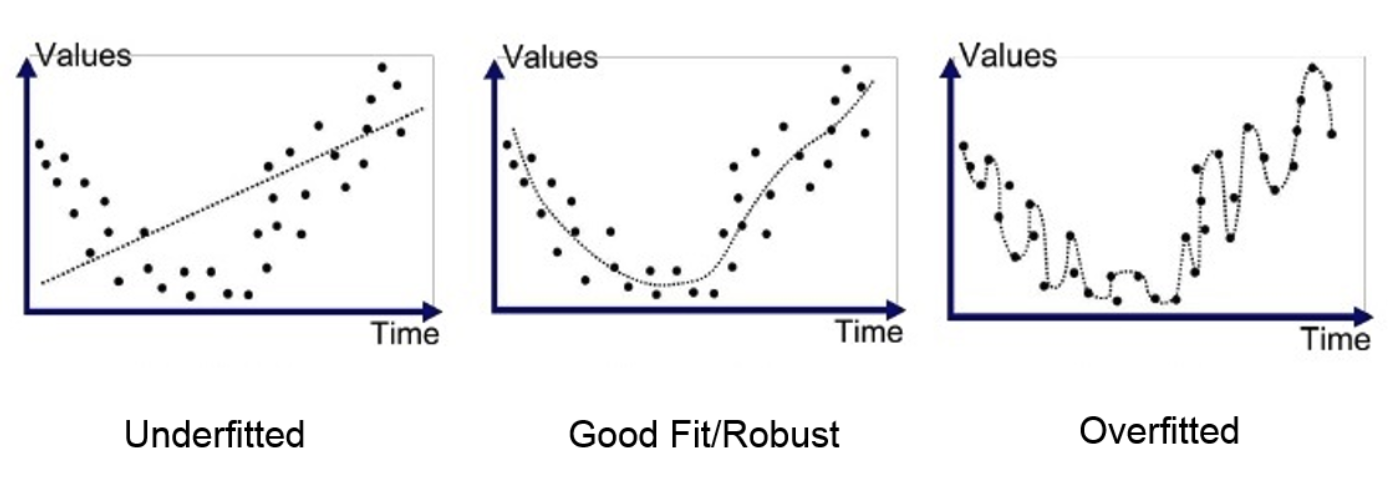
- 1차 모델: 단순한 직선 (Underfitting)
- High Bias, Low Variance
- 트레이닝 에러와 테스트 에러 모두 높음
- 2차 모델: 적절한 복잡도
- Balanced Bias-Variance
- 최적의 예측 성능
- 4차 모델: 과도하게 복잡 (Overfitting)
- Low Bias, High Variance
- 트레이닝 에러는 낮지만 테스트 에러는 높음
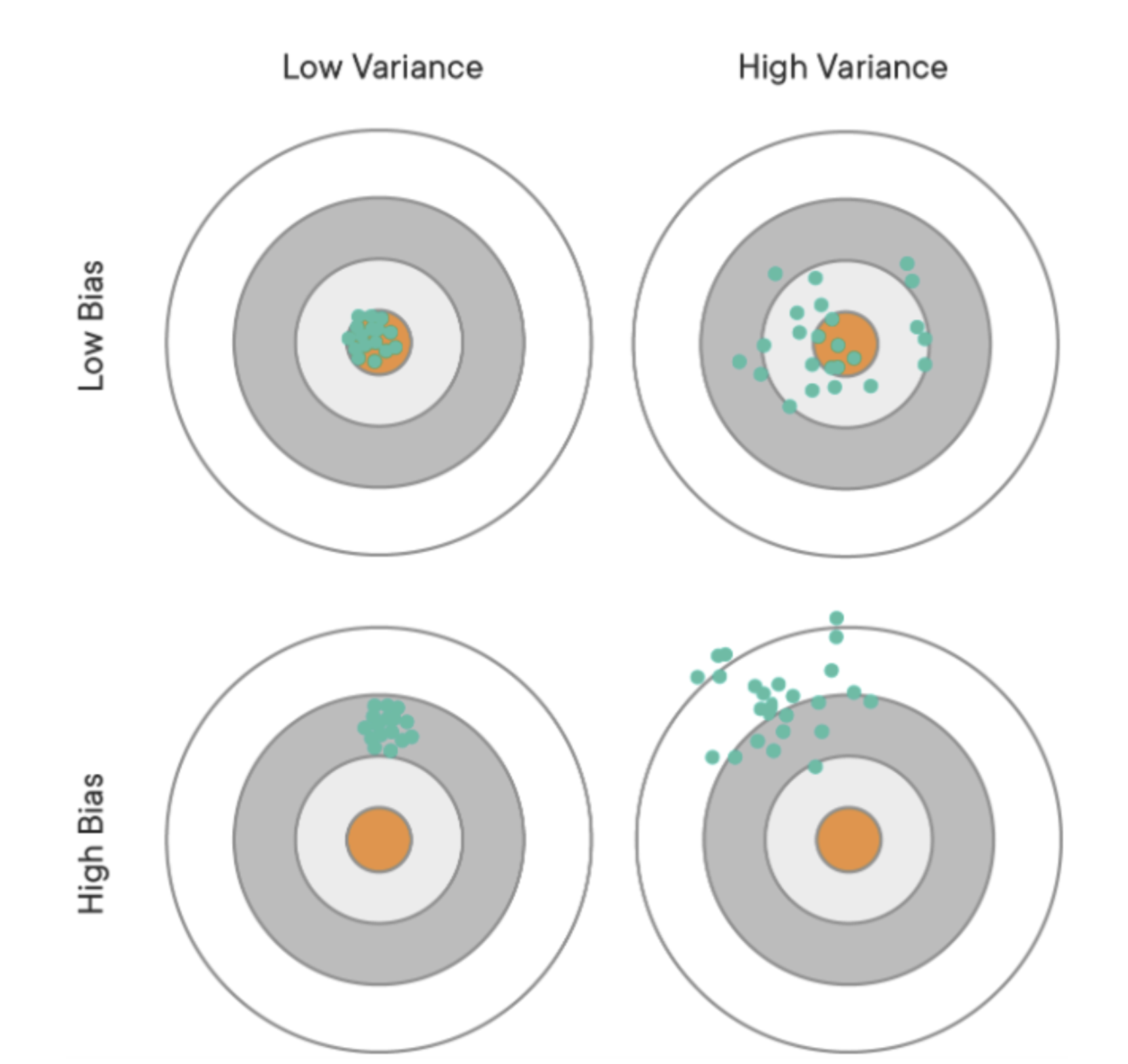
Expected MSE의 분해
Expected MSE = Irreducible Error + Bias² + Variance
- Irreducible Error: 모델로 제어할 수 없는 오차
- Bias: 예측값과 실제값 사이의 체계적 차이
- Variance: 예측값의 변동성
- 단순 선형회귀: y = β₀ + β₁x + ε
- 다중 선형회귀: y = β₀ + β₁x₁ + β₂x₂ + … + βₚxₚ + ε
단순에서 다중으로 갈수록 모델의 복잡도는 증가함.
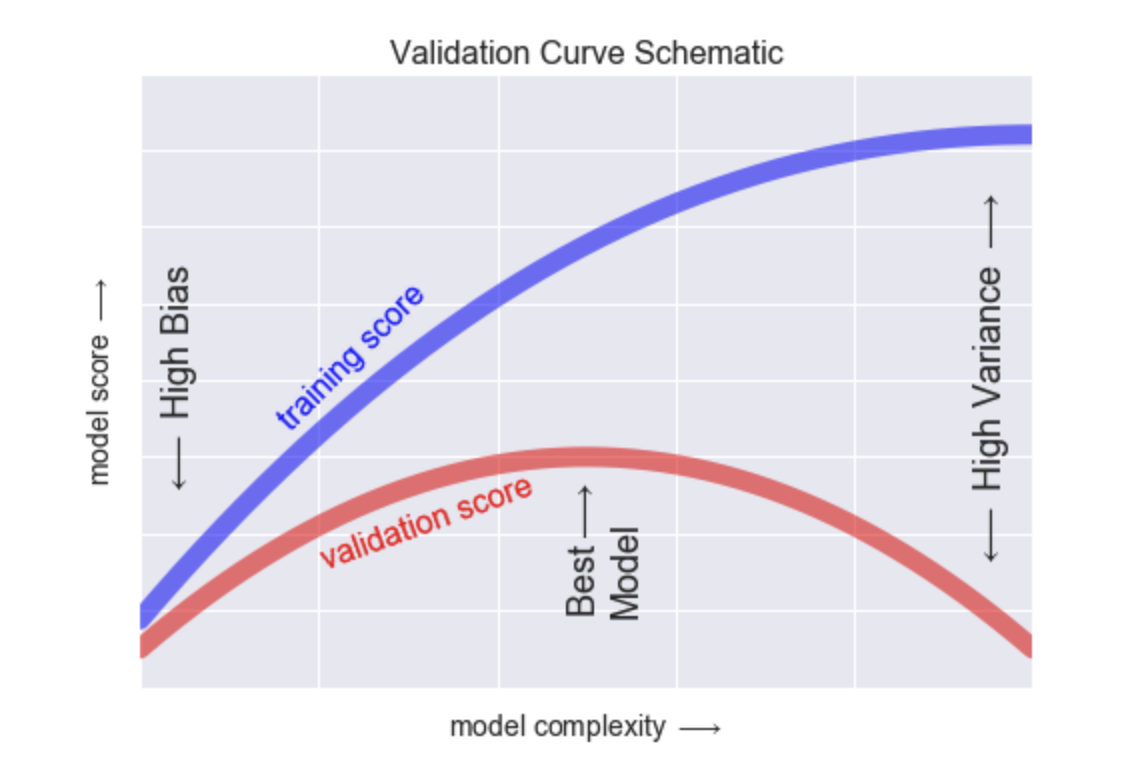
- 모델의 복잡도가 올라갈수록 성능은 초반엔 좋을 수 있지만 점점 성능이 떨어지는 경향이 보임
- 이때 모델의 복잡도가 올라가는 것은 다항식의 항이 많아지는 것을 의미함!
- 그래서 이에 대한 최적점을 찾는 것이 중요함!
그렇다면 이때 최적점을 찾는 방법은 무엇인가?
가장 관련없는 변수부터 제거해본다!
| (β₁, β₂) | β₁² + β₂² | MSE | 제약 만족 여부 | |
|---|---|---|---|---|
| (4, 5) | 41 | 20 | ❌ 위반 (> 30) | |
| (3, 5) | 34 | 23 | ❌ 위반 (> 30) | |
| (4, 4) | 32 | 25 | ❌ 위반 (> 30) | |
| ━━━━━━ | ━━━━━━ | ━━━ | 제약: β₁² + β₂² ≤ 30 | |
| (2, 5) | 27 | 27 | ✅ 만족 | |
| (2, 4) | 18 | 25 | ✅ 만족 ⭐ | |
| (2, 3) | 13 | 29 | ✅ 만족 |
MSE 가 작은게 좋은것! 잊지말기 & 제약조건을 잘 보기

 지혜의 개발공부로그
지혜의 개발공부로그