지혜의 개발공부로그

자료구조, 시간복잡도 Big-O 표기법

14 Jul 2025 | Data Structure

개인공부 후 자료를 남기기 위한 목적임으로 내용 상에 오류가 있을 수 있습니다.

알고리즘

어떤 문제나 목적을 달성하기 위해 거쳐야하는 여러 과정들을 의미. 상황에 맞게 시간 복잡도가 가장 낮은 알고리즘을 선택해 사용하는 것이 중요하다.

일반적으로 알고리즘의 성능 분석은 실행에 필요한 공간 측면에서 분석하는 공간복잡도, 실행 소요시간 측면에서 분석하는 시간복잡도를 추정해 평가한다.

알고리즘의 실행시간

알고리즘의 실행시간은 컴퓨터가 알고리즘 코드를 실행하는 속도에 의존한다. 이떄 이 속도는 컴퓨터 자체의 처리속도, 사용된 언어의 종류, 컴파일러 속도 등에 달려있다.

알고리즘은 하나의 문제를 풀때에도 여러가지 코드를 사용해 풀 수 있다. 문제 풀이에 대한 방법은 여러가지가 있겠지만, 이중에서도 실행시간이 가장 적은 최적의 코드를 짜는 것이 효율적이다. 따라서 알고리즘을 짤 땐 이 시간복잡도라는 것의 중요성이 굉장히 높아진다.

시간복잡도 = 알고리즘의 실행 속도

이러한 시간 복잡도를 보통 점근적 표기법으로 사용되는데 이러한 점근 표기법에는 3가지 종류가 있다.

  1. Big-O표기법: 알고리즘의 최악의 실행시간을 표기
  2. Ω 표기법: 알고리즘의 최상의 실행시간을 표기
  3. Θ 표기법: 알고리즘의 평균 실행시간을 표기

빅오 표기법

불필요한 연산을 제거하여 알고리즘 분석을 쉽게 할 목적으로 사용되는 시간 복잡도 성능 표기법

  • 가장 왼쪽 O(1)으로 갈수록 실행 횟수가 적은 것 > 시간 복잡도가 낮은 것
  • 가장 오른쪽 O(n!)으로 갈수록 실행 횟수가 많은 것 > 시간 복잡도가 높은 것

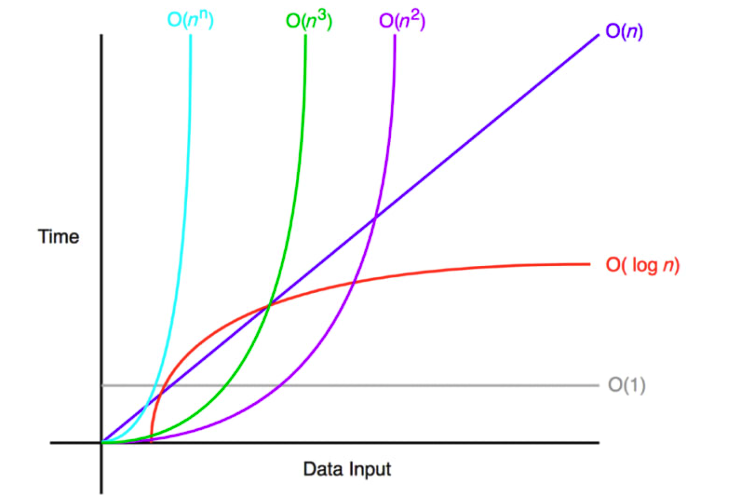
O(1)

입력 데이터 크기에 상관없이 언제나 일정한 시간이 걸리는 알고리즘

def constantTime(n):
    print("Constant는 상수다")

O(n)

입력 데이터의 크기에 비례해 처리 시간이 걸리는 알고리즘

  • n이 한번늘어날 때마다 처리시간이 1 증가 > 선형적 증가
  • n 크리만큼 처리시간이 비례하여 증가
def linearTime(n):
    for i in n:  # > n 
        print(i)

O(n^2)

입력 데이터를 n만큼 반복하는데, 그 안에서 또 n만큼 반복할 때의 표기법 > ex: 2중 포문

  • 데이터가 적을때는 문제없지만, 많아질수록 그래프가 수직상승
  • n만큼 반복하면서 그 안에서 또 n만큼 반복하기에 처리 횟수가 가로, 세로 면적만큼 늘어남
  • n 증가 할때마다 가로와 세로 한줄이 증가하기에 데이터가 커질수록 처리속도 부담도 같이 커짐
def quadraticTime(n):
    for i in n:
        for j in n:
            print(i + j)

O(log N)

이진탐색. 데이터를 찾을 때마다 반틈씩 줄여나가는 알고리즘

  • 전체리스트레서 중간값을 먼저 확인하고 찾는값이 크면 오른쪽으로 검색, 작으면 왼쪽으로 검색
  • 한번 확일할때마다 절반씩 줄여나가며 검색하는 것이 특징
  • O(n) 순차검색보다 훨씬 빠르다
  • 데이터가 증가해도 성능에 크게 영향을 주지 않는다
def binary_search(n):
    count = 0  # > +1
    i = n  # > +1
    while i > 0:
        count += 1  # > +2
        i = i // 2
    return count

Related Posts