지혜의 개발공부로그

NumPy 브로드캐스팅 규칙

10 Jul 2025 | DA

개인공부 후 자료를 남기기 위한 목적임으로 내용 상에 오류가 있을 수 있습니다.

브로드캐스팅

일반적으로 NumPy는 모양이 다른 배열끼리의 연산은 불가능하다.

a = np.array([1,2,3])
b = np.array([1,2])
a + b

ValueError Traceback (most recent call last) in <module>()----> 1 a + bValueError: operands could not be broadcast together with shapes (3,) (2,)

에러에서도 보면 브로드캐스트가 되지 못했다는 것을 보여주고 있다. 그렇다는 것은 어떤 특정 조건이 맞아진다면 모양이 다른 배열끼리도 연산을 수행할 수 있다는 것을 의미한다.

  1. 차원 수가 다른 경우: 작은 차원의 배열 앞쪽에 크기 1인 차원을 추가
  2. 각 차원을 뒤에서부터 비교: 각 차원의 크기가 같거나, 둘 중 하나가 1이어야 함
  3. 호환되지 않으면: 브로드캐스팅 불가능

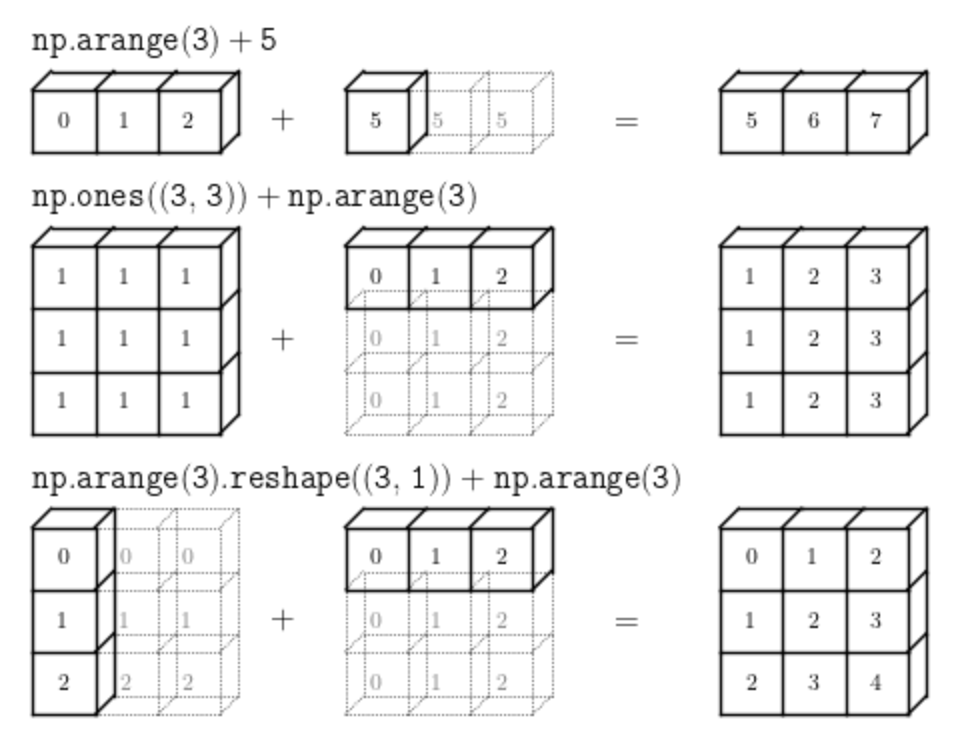
코드로 보면 아래와 같다.

# 1차원 배열과 2차원 배열 
a = np.array([1, 2, 3])
b = np.array([[10, 120, 120], [80, 120, 100], [60, 90, 80]])

print(a*b)
# [[ 10 240 360]
#  [ 80 240 300]
#  [ 60 180 240]]

(3,3) 배열과 (3,)끼리 곱하려니 (3,) 행렬이 (1,3)행렬로 확장된 후, 다시 (3,3)로 확장 및 복사 되어 계산된 것을 볼 수 있다.

이처럼 브로드캐스팅을 통해 크기가 다른 배열들도 연산이 가능해진다. NumPy가 자동으로 작은 배열을 큰 배열의 형태에 맞춰 확장해주는 개념인 것이다!

# 스칼라와 배열
a = np.array([1,2,3,4])
b = 10

a + b  # > [11,12,13,14]

# 서로 다른 차원
a = np.array([[1],
              [2],
              [3]])  # (3,1)
b = np.array([10,20])  # (2.)

a + b  # (3,2)
# >  [[11, 21],
#     [12, 22],
#     [13, 23]]

브로드캐스팅이 일어나는 과정

위 코드 예시에서처럼 서로 다른 차원의 배열이 더해진다고 생각해보자. > (3,1)배열과 (2,)배열

  1. (2,)배열이 (1,2)배열로 차원이 추가된다
  2. (3,1)배열과 (1,2) 배열을 비교해 브로드캐스팅이 됨을 확인
  3. 첫번째 차원: (3,1) 베열 > (3,3)으로 확장
  4. 두번쨰 차원: (1,2) 배열 > (2,2)으로 확장
  5. 최종: (3,2) 형태로 확장

브로드캐스팅의 장점

  • 메모리 효율성: 실제 배열을 복사하지 않고 가상으로 확장하기에
  • 코드 간결성: 반복문 없이 배열 전체의 연산이 가능
  • 성능: C로 구현된 최적화된 연산을 활용

Related Posts